- 11.
- We beschouwen de voorvallen
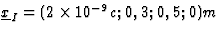 en
en 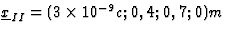 . (Let op:
alleen hier lees voor c, s/m, en in deze uitwerking is de eerste
component van de 4-vector de tijd of het tijdsverschil, en niet als gewoonlijk
tijd maal lichtsnelheid -- sorry voor de verwarring).
. (Let op:
alleen hier lees voor c, s/m, en in deze uitwerking is de eerste
component van de 4-vector de tijd of het tijdsverschil, en niet als gewoonlijk
tijd maal lichtsnelheid -- sorry voor de verwarring).
- a.
- Voor de verschil-viervector
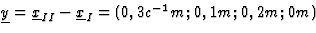 geldt
y2=(0,09-(0,01+0,04))m2=0,04 m2>0. De voorvallen zijn tijdachtig
gescheiden, derhalve kan II veroorzaakt zijn door I. (Immers, de ruimtelijke
afstand bedraagt 0,224m, het tijdsverschil bedraagt 0,3c-1m. In deze
tijd kan een lichtsignaal van I naar II, dus I en II zijn causaal verbonden.
geldt
y2=(0,09-(0,01+0,04))m2=0,04 m2>0. De voorvallen zijn tijdachtig
gescheiden, derhalve kan II veroorzaakt zijn door I. (Immers, de ruimtelijke
afstand bedraagt 0,224m, het tijdsverschil bedraagt 0,3c-1m. In deze
tijd kan een lichtsignaal van I naar II, dus I en II zijn causaal verbonden.
- b.
- Als er een stelsel S' bestaat waarin I en II gelijktijdig zijn, is er een
standaard Lorentz transformatie L (verschil-viervectoren transformeren altijd onder een
homogene, standaard Lorentz transformatie) van S naar S' zodat
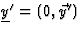 .
Dan y'2 <0. We hadden echter y2>0. Aangezien iedere Lorentz transformatie y2 invariant
laat is zo'n Lorentz transformatie er niet.
.
Dan y'2 <0. We hadden echter y2>0. Aangezien iedere Lorentz transformatie y2 invariant
laat is zo'n Lorentz transformatie er niet.
- c.
- Er is wel een stelsel S'' waarin I en II gelijke ruimtelijke posities
hebben. S'' is met S gerelateerd via een standaard
Lorentz transformatie. We willen
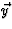 "=0.
Dan geldt
"=0.
Dan geldt 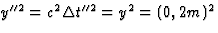 . Dus
y0"=
. Dus
y0"=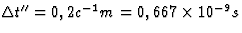 .
S'' beweegt in de richting van
.
S'' beweegt in de richting van 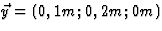 .
De grootte van de snelheid is
.
De grootte van de snelheid is 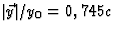 . (Dat
dit werkt is als volgt in te zien: we draaien
. (Dat
dit werkt is als volgt in te zien: we draaien
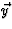 naar de positieve
naar de positieve
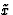 -as van een hulpstelsel
-as van een hulpstelsel 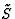 , zodat
, zodat 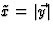 , en
we voeren een Lorentz transformatie met snelheid w in deze richting uit. Dan
geldt
, en
we voeren een Lorentz transformatie met snelheid w in deze richting uit. Dan
geldt 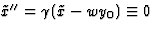 . Hieruit volgt de grootte van
de snelheid
. Hieruit volgt de grootte van
de snelheid 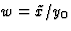 . Na terugdraaien geldt
. Na terugdraaien geldt 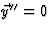 , zodat I en
II gelijke ruimtelijke posities hebben gekregen in S''.)
, zodat I en
II gelijke ruimtelijke posities hebben gekregen in S''.)
- d.
- i.
- De verschil-viervector is
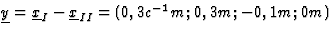 . Voor de
lengte van de viervector
. Voor de
lengte van de viervector 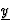 geldt nu y2=(0,32-(0,32+0,12))
m2=-(0,1 m)2<0.
geldt nu y2=(0,32-(0,32+0,12))
m2=-(0,1 m)2<0. 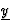 is dus een ruimteachtige vector. De
voorvallen I en II zijn derhalve ruimtelijk gescheiden en kunnen dus niet
causaal verbonden zijn.
is dus een ruimteachtige vector. De
voorvallen I en II zijn derhalve ruimtelijk gescheiden en kunnen dus niet
causaal verbonden zijn.
- ii.
- Er is een stelsel waarin I en II gelijktijdig zijn. We zoeken weer
een geschikte Lorentz transformatie L. Voor gelijktijdigheid eisen we nu
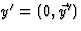 .Er geldt dan
.Er geldt dan 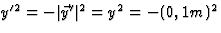 . Dit geeft de afstand
. Dit geeft de afstand
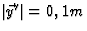 in S'. Om de Lorentz transformatie te vinden gaan we weer in een stelsel
zitten waarin de ruimtelijke verschil-vector langs de
in S'. Om de Lorentz transformatie te vinden gaan we weer in een stelsel
zitten waarin de ruimtelijke verschil-vector langs de 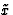 -as ligt,
zodat
-as ligt,
zodat 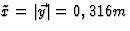 . Langs deze as voeren we de Lorentz transformatie uit, de
richting ervan wordt dus weer gegeven door
. Langs deze as voeren we de Lorentz transformatie uit, de
richting ervan wordt dus weer gegeven door 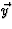 . We willen
. We willen 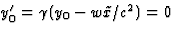 . Hieruit volgt direct
. Hieruit volgt direct 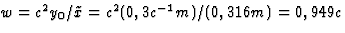 . De standaard Lorentz transformatie die I en II relateert is nu bepaald.
. De standaard Lorentz transformatie die I en II relateert is nu bepaald.
- iii.
- Een stelsel S'' waarin I en II gelijke ruimtelijke posities
hebben is er niet, dan zou immers voor
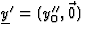 gelden
y''2=c2y''20>0. Dit laatste is in tegenspraak met y''2=y2<0.
gelden
y''2=c2y''20>0. Dit laatste is in tegenspraak met y''2=y2<0.
Zie ook de uitwerking van
opgave 19
uit de syllabus.
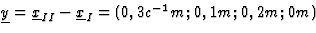 geldt
y2=(0,09-(0,01+0,04))m2=0,04 m2>0. De voorvallen zijn tijdachtig
gescheiden, derhalve kan II veroorzaakt zijn door I. (Immers, de ruimtelijke
afstand bedraagt 0,224m, het tijdsverschil bedraagt 0,3c-1m. In deze
tijd kan een lichtsignaal van I naar II, dus I en II zijn causaal verbonden.
geldt
y2=(0,09-(0,01+0,04))m2=0,04 m2>0. De voorvallen zijn tijdachtig
gescheiden, derhalve kan II veroorzaakt zijn door I. (Immers, de ruimtelijke
afstand bedraagt 0,224m, het tijdsverschil bedraagt 0,3c-1m. In deze
tijd kan een lichtsignaal van I naar II, dus I en II zijn causaal verbonden.
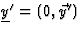 .
Dan y'2 <0. We hadden echter y2>0. Aangezien iedere Lorentz transformatie y2 invariant
laat is zo'n Lorentz transformatie er niet.
.
Dan y'2 <0. We hadden echter y2>0. Aangezien iedere Lorentz transformatie y2 invariant
laat is zo'n Lorentz transformatie er niet.
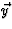 "=0.
Dan geldt
"=0.
Dan geldt 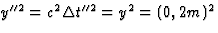 . Dus
y0"=
. Dus
y0"=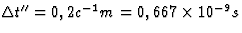 .
S'' beweegt in de richting van
.
S'' beweegt in de richting van 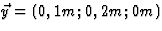 .
De grootte van de snelheid is
.
De grootte van de snelheid is 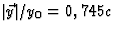 . (Dat
dit werkt is als volgt in te zien: we draaien
. (Dat
dit werkt is als volgt in te zien: we draaien
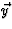 naar de positieve
naar de positieve
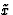 -as van een hulpstelsel
-as van een hulpstelsel 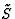 , zodat
, zodat 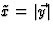 , en
we voeren een Lorentz transformatie met snelheid w in deze richting uit. Dan
geldt
, en
we voeren een Lorentz transformatie met snelheid w in deze richting uit. Dan
geldt 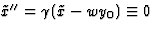 . Hieruit volgt de grootte van
de snelheid
. Hieruit volgt de grootte van
de snelheid 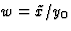 . Na terugdraaien geldt
. Na terugdraaien geldt 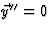 , zodat I en
II gelijke ruimtelijke posities hebben gekregen in S''.)
, zodat I en
II gelijke ruimtelijke posities hebben gekregen in S''.)
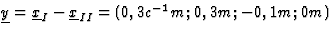 . Voor de
lengte van de viervector
. Voor de
lengte van de viervector 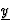 geldt nu y2=(0,32-(0,32+0,12))
m2=-(0,1 m)2<0.
geldt nu y2=(0,32-(0,32+0,12))
m2=-(0,1 m)2<0. 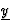 is dus een ruimteachtige vector. De
voorvallen I en II zijn derhalve ruimtelijk gescheiden en kunnen dus niet
causaal verbonden zijn.
is dus een ruimteachtige vector. De
voorvallen I en II zijn derhalve ruimtelijk gescheiden en kunnen dus niet
causaal verbonden zijn.
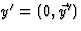 .Er geldt dan
.Er geldt dan 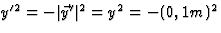 . Dit geeft de afstand
. Dit geeft de afstand
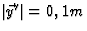 in S'. Om de Lorentz transformatie te vinden gaan we weer in een stelsel
zitten waarin de ruimtelijke verschil-vector langs de
in S'. Om de Lorentz transformatie te vinden gaan we weer in een stelsel
zitten waarin de ruimtelijke verschil-vector langs de 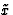 -as ligt,
zodat
-as ligt,
zodat 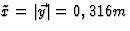 . Langs deze as voeren we de Lorentz transformatie uit, de
richting ervan wordt dus weer gegeven door
. Langs deze as voeren we de Lorentz transformatie uit, de
richting ervan wordt dus weer gegeven door 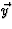 . We willen
. We willen 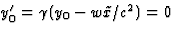 . Hieruit volgt direct
. Hieruit volgt direct 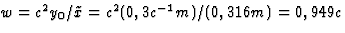 . De standaard Lorentz transformatie die I en II relateert is nu bepaald.
. De standaard Lorentz transformatie die I en II relateert is nu bepaald.
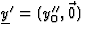 gelden
y''2=c2y''20>0. Dit laatste is in tegenspraak met y''2=y2<0.
gelden
y''2=c2y''20>0. Dit laatste is in tegenspraak met y''2=y2<0.