Up: Topics

Toevalsmatrixtheorie: Orde in Chaos

Op 15 februari 2000 vond in de Nieuwe Kerk in Den Haag de feestelijke uitreiking plaats van de NWO/SPINOZA premies. De uitreiking door minister Hermans werd voorafgegaan door lezingen van de vier prijswinnaars. Hier volgt een iets bekorte versie van de lezing van Carlo Beenakker.

Vijfhonderd jaar geleden maakte Albrecht Dürer de geestelijke wereld van wetenschap en kunst aanschouwelijk in een gravure getiteld Melancholie. Er valt een hoop te zien, maar vanmiddag wilde ik uw aandacht speciaal vragen voor het vierkant in de rechterbovenhoek. Misschien heeft u hier wel eens mee gepuzzeld; het heet een magisch vierkant, omdat de getallen in het vierkant dezelfde som hebben, of je ze nu van links naar rechts optelt, van boven naar onder, of diagonaal. Zo'n vierkant met getallen noemen wiskundigen een matrix. De getallen in een magische matrix zijn heel speciaal gekozen. Ze staan daar niet toevallig. Stelt u zich eens voor dat u de getallen door het toeval, bijvoorbeeld door een dobbelsteen, zou laten aanwijzen. Het resultaat is ongetwijfeld geen magisch vierkant zoals bij Dürer; en toch heeft zo'n toevalsmatrix voor mij heel bijzondere, ik zou haast zeggen magische eigenschappen.

Chaotische beweging

Mijn fascinatie voor toevalsmatrices ontstond een aantal jaren geleden, in een zoektocht naar een theorie voor de chaotische beweging van elektronen. Chaos is het tegendeel van orde, dat is zo in het gewone spraakgebruik -"je kamer is een chaos, breng 't op orde" - en ook zo in de natuurkunde. Het verschil tussen chaotische en geordende beweging is in één oogopslag te zien als je je het elektron voorstelt als een biljartbal. De beweging op een cirkelvormige biljarttafel levert een prachtig geordende figuur op; een vertrouwd gezicht voor wie wel eens met Spirograaf gespeeld heeft. Maar zie wat er gebeurt als de boven- en onderkant van de biljarttafel worden afgeplat: er ontstaat een wirwar van paden, complete chaos.

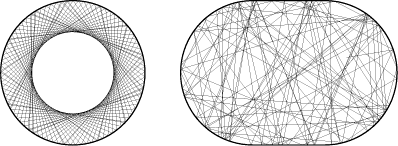
Als je er even over nadenkt is het heel verassend. Je zou misschien gedacht hebben dat een grillige vorm noodzakelijk is voor chaotische beweging, maar niets is minder waar. Het rechterbiljart heeft nog steeds een fraaie symmetrische vorm, twee halve cirkels verbonden met evenwijdige rechte lijnstukken. (Het lijkt op een voetbalstadium.) Toch is elke symmetrie uit de beweging verdwenen. Wat er aan de hand is, is dat in het cirkelvormige biljart bij elke botsing met de wand zowel de grootte als de richting van de snelheid (ten opzichte van de wand) dezelfde blijft. In het stadiumvormige biljart blijft alleen de grootte dezelfde. De richting varieert op een onvoorspelbare, chaotische wijze van de ene botsing naar de andere.

Dit inzicht, dat chaos kan optreden in een omgeving die er op het eerste gezicht heel geordend uitziet, heeft onze kijk op de wereld fundamenteel veranderd. Chaos is de reden dat weersvoorspellingen niet langer dan een paar dagen vooruit kunnen kijken. Net zoals de beweging in het stadiumvormige biljart na een paar botsingen onvoorspelbaar is geworden. Het gaat hier om het optreden van chaos in macroscopische systemen. Macroscopisch, dat is de wereld om ons heen, die we met het blote oog kunnen zien. Een biljarttafel in een café is een macroscopisch voorwerp.

Biljarten met elektronen

Een biljart voor elektronen is een mesoscopisch voorwerp. Mesoscopisch, dat is de wereld die te klein is om met het blote oog te zien, maar toch niet zo klein dat je de afzonderlijke atomen en moleculen kunt onderscheiden. "Mesos" = midden, want mesoscopisch zit midden tussen macroscopisch en microscopisch in. Het is een term die ontstaan is vanuit de elektronische industrie, in ons land Philips, waar ik het vak geleerd heb. Mesoscopische voorwerpen hebben afmetingen tussen een duizendste en een miljoenste millimeter. Een computerchip is nu nog een macroscopisch voorwerp, maar het zal niet lang meer duren of de miniaturisatie van de elektronica zal ons in de mesoscopische wereld binnenvoeren. Mesoscopische elektrische componenten staan nog niet in de winkel, maar we kunnen ze wel bestuderen in het laboratorium.

Hier ziet u zo'n mesoscopisch voorwerp, een biljart voor elektronen, gefabriceerd in een laboratorium van de universiteit van Harvard in de Verenigde Staten. [Gepubliceerd in: M.J. Berry, J.A. Katine, R.M. Westervelt, and A.C. Gossard, Phys.Rev. B 50, 17721 (1994).] In ons land worden soortgelijke componenten bij de TU Delft gefabriceerd. Het is een simpel ontwerp: een cirkelvormig gebied (doorsnede 1/1000 mm) waar de elektronen in kunnen rondlopen en twee openingen waardoor ze het gebied kunnen verlaten. Net als in een echt biljart, verwachten we dat de beweging van de elektronen in dit cirkelvormige gebied geordend is, terwijl chaotische beweging op zou moeten treden als we de vorm veranderen in die van een stadium. Maar nu stoten we op een diepzinnig probleem: Het elektron is geen biljartbal.

Quantumchaos

Nogal logisch, zult u denken, maar wat ik bedoel te zeggen is dit: Een elektron heeft geen precieze baan, zoals een biljartbal, maar kan op meerdere plaatsen tegelijkertijd zijn, zoals het licht van een kaars. Dit is een van de grootste ontdekkingen van de twintigste eeuw, dat de wetten van de klassieke mechanica (de wetten van Newton, die de baan van een biljartbal beschrijven) op hele kleine afstanden vervangen moeten worden door de wetten van de quantummechanica. In de quantummechanica volgen deeltjes geen banen, maar verspreiden zich als golven. Van een golf kun je niet zeggen hij is hier of daar, een golf is overal. Zo brengt het biljart voor elektronen ons tot de fundamentele vraag, wat de betekenis is van het begrip chaos in de quantummechanica. Kun je nog wel onderscheid maken tussen chaotische en geordende beweging als je geen paden meer kunt tekenen? Het was deze zoektocht naar de quantumchaos die mij bracht tot de toevalsmatrices en hun magische eigenschappen.

De matrix waar het hier over gaat, bevat in het eenvoudigste geval vier getallen:

r	t
t	r'

De naam van dit vierkant is de verstrooiingsmatrix. De getallen r en r' geven de kans aan dat het elektron door dezelfde opening het biljart verlaat als waardoor het binnenkwam. (Er zijn twee openingen, dus twee getallen.) Dit zijn de reflectiekansen. Het getal t geeft de kans aan dat het elektron via de ene opening het biljart binnenkomt en via de andere opening vertrekt. Dit is de transmissiekans. De getallen in de verstrooiingsmatrix zijn complexe getallen, die zowel informatie bevatten over de amplitude van de elektrongolf als over de fase. (De wortel uit min één is een voorbeeld van een complex getal.) De kans is een gewoon getal tussen 0 en 1 dat je kunt vinden door het kwadraat te nemen van de absolute waarde van het complexe getal. Niet alle complexe getallen kunnen voorkomen in de verstrooiingsmatrix. Omdat het elektron òf door de ene òf door de andere opening moet vertrekken, zullen de kansen langs een rij of een kolom moeten optellen tot 1. Oftewel, reflectie- en transmissiekans zijn samen gelijk aan 1. We zeggen dat de verstrooiingsmatrix een unitaire matrix is. Het lijkt op een magisch vierkant, maar dan met complexe getallen in plaats van gehele getallen. ( Er is nog een verschil met een magisch vierkant: de som van de diagonalen in een unitaire matrix ligt niet vast. In plaats daarvan geldt dat elk paar rijen of kolommen, opgevat als vectoren, loodrecht op elkaar moet staan.)

Het ei van Columbus

De precieze waarde van de reflectie- en transmissiekansen hangt af van de precieze vorm en grootte van het biljart. In het laboratorium heb je die vorm en grootte niet precies onder controle en ben je dus eigenlijk vooral geïnteresseerd in de statistische verdeling van die kansen. Wat is de vaakst voorkomende waarde van de transmissiekans in een chaotisch biljart? Daar kan de toevalsmatrixtheorie een heel precies antwoord op geven.

We beschrijven een chaotisch biljart door de getallen in de verstrooiingsmatrix volledig toevallig te kiezen - als het maar een unitaire matrix blijft. Dat is het ei van Columbus: een beschrijving van chaos die niet uitgaat van beweging langs paden. Net zoals dat beroemde ei, is het een heel eenvoudige oplossing, maar de gevolgen zijn onverwacht. Je zou misschien vermoeden dat de vaakst voorkomende waarde van de transmissiekans 1/2 is. Het lijkt immers op het gooien van kruis of munt: ofwel het elektron keert terug door de opening waardoor hij is binnengekomen, ofwel hij gaat weg door de andere opening, en voor wanordelijke paden zou je een kans 1/2 voor elk van beide gebeurtenissen verwachten. Maar dit vermoeden is onjuist: de vaakst voorkomende waarde van de transmissiekans is 0 en niet 1/2. Om precies te zijn, de statistische verdeling van de transmissiekans is omgekeerd evenredig met de wortel uit de transmissiekans, dus gepiekt rond transmissiekans nul. Deze verassende voorspelling van de toevalsmatrixtheorie is nauwkeurig door computersimulaties geverifieerd. (meer informatie)

Lokalisatie

Kennelijk is chaos voor een elektron iets anders dan voor een biljartbal. Het elektron herinnert zich langs welke opening hij het biljart is binnengekomen en keert met hoge waarschijnlijkheid naar dezelfde opening terug, zelfs al lijkt de beweging in het biljart volledig onvoorspelbaar. Stel je eens voor dat het elektron in plaats van in een biljart op een roulettewiel zou bewegen. Hij vertrekt van geluksgetal 7, het wiel draait, hij springt op een chaotische manier van het ene nummer naar het andere, riens ne va plus, het wiel komt tot rust, en zie: het elektron is weer terug op geluksgetal 7. Zo wonderlijk is de quantummechanica.

De term die natuurkundigen voor dit gedrag gebruiken is lokalisatie. Lokalisatie wil zeggen dat het elektron met hoge waarschijnlijkheid terugkeert naar zijn vertrekpunt, dus gelokaliseerd is rond zijn vertrekpunt. Lokalisatie is een gevolg van het golfkarakter van het elektron. De golven versterken elkaar rond het vertrekpunt, maar daarbuiten doven ze elkaar uit, zoals licht plus licht gelijk kan zijn aan donker. Omdat lokalisatie een golfverschijnsel is, zouden ook andere golven het moeten vertonen. Lichtgolven, bijvoorbeeld, of geluidsgolven. De theorie van chaos en lokalisatie is in deze bredere context nog onontwikkeld. Ik zie toevalsmatrices als een instrument bij uitstek om tot een universele theorie van chaotische golven te komen, en wil de NWO/SPINOZA-premie aanwenden om dit doel te bereiken.

Up: Topics