In onze groep is een nieuwe methode ontwikkeld om een gecompliceerd probleem uit de vaste-stoffysica op te lossen. Het probleem waar het om gaat, is de berekening van het geleidingsvermogen van een metaalkorrel. Dit probleem is gecompliceerd omdat de beweging van elektronen in de korrel afhangt van waar de verontreinigingen zich bevinden. Aangezien elke korrel anders is, is het niet zo zinvol om het geleidingsvermogen van een enkele korrel te weten. De kansverdeling van het geleidingsvermogen, daar gaat het om. De gangbare methode om de kansverdeling te vinden, gaat uit van een groot aantal korrels, elk met een verschillende configuratie van verontreinigingen. Voor elk van die korrels wordt een quantummechanisch verstrooiingsprobleem opgelost. Dit bestaat uit het berekenen van een matrix van complexe getallen. Het geleidingsvermogen wordt door deze zogenaamde verstrooiingsmatrix bepaald via een formule die teruggaat op werk van R. Landauer van IBM. Door deze berekening voor heel veel korrels te herhalen, vindt men uiteindelijk de kansverdeling van het geleidingsvermogen. De vondst van de Leidse onderzoeksgroep voor mesoscopische fysica, samenwerkend met het Centre d'Etudes de Saclay (Frankrijk), is dat deze hele procedure aanmerkelijk verkort en vereenvoudigd kan worden. De meest tijdrovende en ingewikkelde stap is namelijk de berekening van de verstrooiingsmatrix voor elk van de korrels. Nadat je één zo'n matrix met veel moeite berekend hebt, valt er in de elementen geen systematiek te ontdekken; het lijkt wel alsof het getallen uit de loterij zijn. Dit suggereert om die hele berekening dan maar achterwege te laten en de matrixelementen door het toeval te laten aanwijzen. Deze aanpak heet toevalsmatrixtheorie.
In de mathematische fysica heeft men lang geleden de statistische eigenschappen van matrices met toevallig gekozen elementen onderzocht. Een beroemde wet van E.P. Wigner en F.J. Dyson uit de zestiger jaren stelt dat de eigenwaarden van zo'n toevalsmatrix elkaar afstoten alsof het gelijk geladen deeltjes zijn. Door deze wet te combineren met de formule van Landauer volgt meteen de kansverdeling P van het geleidingsvermogen G. In het eenvoudigste geval dat de stroom door de korrel via een heel nauw puntcontact loopt, is het resultaat: P=G-1+2/b voor G<2e2/h en P=0 voor G>2e2/h. Het getal b is 2 of 1, afhankelijk van of er wel of geen magneetveld aanwezig is. Het bijzondere van deze kansverdeling is dat er helemaal geen eigenschappen van de metaalkorrel in voorkomen, zoals de grootte, de vorm, het soort metaal, het aantal verontreinigingen, enzovoorts. De kansverdeling hangt alleen maar af van het getal b en de natuurconstanten e (de elektronlading) en h (de constante van Planck). Zo'n onafhankelijkheid van materiaaleigenschappen noemen natuurkundigen "universaliteit". Het is iets bijzonders. De meeste natuurverschijnselen zijn in het geheel niet universeel.
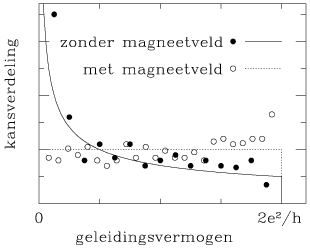
Als die kansverdeling universeel is, zou het niet moeilijk moeten zijn om haar experimenteel te toetsen. Immers, het zou niet uit mogen maken welk systeem je bekijkt. Hoewel verschillende groepen aan het proberen zijn, de voorspelde kansverdeling te meten, is het toch niet eenvoudig gebleken. De moeilijkheid is, dat de temperatuur heel laag moet zijn - vlak bij het absolute nulpunt. Bij hogere temperaturen worden de quantummechanische fluctuaties in het geleidingsvermogen onderdrukt. Het zijn juist deze fluctuaties, die de kansverdeling haar karakteristieke vorm geven. Wat inmiddels wel mogelijk is gebleken, is een test van de theorie door middel van een computersimulatie. Op een computer is het makkelijk de toestand van het absolute nulpunt na te bootsen. Zoals te zien is in de figuur, is er een goede overeenstemming tussen theorie en simulatie. Zo heeft de oude wiskundige theorie van toevalsmatrices een nieuwe en onverwachte toepassing gevonden.
Kansverdeling van het geleidingsvermogen van een metaalkorrel. De getrokken en gestippelde lijnen zijn de voorspellingen van de toevalsmatrixtheorie; de open en dichte rondjes zijn de resultaten van een computersimulatie (uitgevoerd door H.U. Baranger en P.A. Mello). In aanwezigheid van een magneetveld is elke waarde van het geleidingsvermogen tussen 0 en 2e2/h even waarschijnlijk. Zonder magneetveld zijn kleine waarden waarschijnlijker dan grote. |
Literatuur
R.A. Jalabert, J.-L. Pichard en C.W.J. Beenakker, Europhysics Letters 27 (1994) 255.
H.U. Baranger en P.A. Mello, Physical Review Letters 73 (1994) 142.