5. Algemene Lorentz transformaties

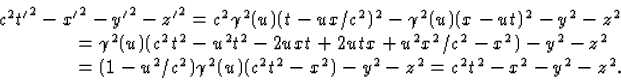
Standaard Lorentz transformaties in de x-, y- en z-richting geven een verband tussen inertiaalsystemen waarbij de lichtsnelheid niet verandert. We kunnen in feite algemeen nagaan dat de door formule (4.41) gegeven standaard Lorentz transformatie in een willekeurige richting deze eigenschap heeft. Dit zijn niet de enige lineaire transformaties van de ruimte-tijd die deze eigenschap hebben. Als we bijvoorbeeld eerst een standaard Lorentz transformatie in de x-richting uitvoeren en vervolgens een standaard Lorentz transformatie in de y-richting, dan geeft dit samen een transformatie die nog steeds de lichtsnelheid onveranderd laat, maar die toch niet gelijk blijkt te zijn aan een standaard Lorentz transformatie in een bepaalde richting.

Opgave 14:

Voer eerst een Lorentz transformatie uit in de x-richting en daarna een Lorentz transformatie in de y-richting. Neem voor het gemak u gelijk voor beide transformaties. Laat zien dat er geen $\vec u$ bestaat zodanig dat deze combinatie van twee simpele Lorentz transformaties van de vorm is zoals gegeven in formule (4.41). (Het is een combinatie van zo'n Lorentz transformatie en een draaiing, maar dat hoeft U hier niet te laten zien.)

We willen nu een algemene karakterisering geven van lineaire transformaties van ruimte-tijd coördinaten die in de Einsteinse relativiteitstheorie toegelaten zijn voor de beschrijving van het verband tussen inertiaalsystemen. Daartoe bekijken we de volgende kwadratische uitdrukking in de ruimte-tijdcoördinaten x, y, z en t van een gebeurtenis:

c2t2-x2-y2-z2. (5.1)

Deze kwadratische vorm heeft twee belangrijke eigenschappen. De eerste eigenschap is invariantie onder standaard Lorentz transformaties. Dat wil zeggen dat voor zo'n transformatie van x, y, z, t naar x', y', z', t' geldt

c2t2-x2-y2-z2=c2t'2-x'2-y'2-z'2. (5.2)

We gaan dit even na voor het geval van een transformatie in de x-richting, dus een transformatie volgens formule (4.37)
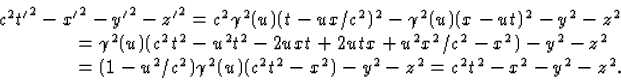
\begin{array} c^2{t'}^2-{x'}^2-{y'}^2-{z'}^2 =c^2\gamma^... ...)\gamma^2(u)(c^2t^2-x^2)-y^2-z^2=c^2t^2-x^2-y^2-z^2.\end{array} (5.3)

De tweede belangrijke eigenschap luidt als volgt: Iedere lineaire transformatie van ruimte-tijd coördinaten die de kwadratische vorm invariant laat, laat ook de lichtsnelheid onveranderd. Ook dit gaan we na: Een punt van het front van een lichtgolf beweegt zich eenparig rechtlijnig met snelheid c. De wereldlijn van zo'n punt is een rechte lijn in de 4-dimensionale ruimte-tijd gegeven door de formules
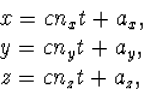
\begin{array} x=cn_xt+a_x,\\ y=cn_yt+a_y,\\ z=cn_zt+a_z,\end{array} (5.4)

met daarin nx, ny, nz de componenten van de eenheidsvector $\vec n$ die de richting van de beweging aangeeft, en ax, ay, az constanten, de waarden van de ruimtecoördinaten op t=0. Bezie twee willekeurige verschillende gebeurtenissen op deze wereldlijn, met ruimte-tijd coördinaten x1, y1, z1, t1 en x2, y2, z2, t2. Daarvoor geldt
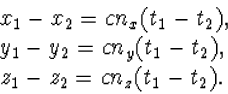\begin{array} x_1-x_2=cn_x(t_1-t_2),\\ y_1-y_2=cn_y(t_1-t_2),\\ z_1-z_2=cn_z(t_1-t_2).\end{array} (5.5)

Kwadrateren en optellen geeft

(x2-x1)2+(y2-y1)2+(z2-z1)2=c2(t2-t1)2, (5.6)

oftewel

c2(t2-t1)2-(x2-x1)2-(y2-y1)2-(z2-z1)2=0. (5.7)

Er is een lineaire transfomatie x, y, z, t $\rightarrow$ x', y', z', t'. Ook in de nieuwe ruimte-tijd coördinaten beweegt het golffrontpunt zich eenparig rechtlijnig, met een snelheid die we $\vec v{\,}'=(v_x^\prime,v_y^\prime,v_z^\prime)$ noemen. De wereldlijn wordt weer beschreven door formules van de vorm (5.4)
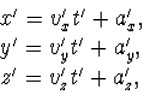\begin{array} x'=v_x^\prime t'+a_x^\prime,\\ y'=v_y^\prime t'+a_y^\prime, \\ z'=v_z^\prime t'+a_z^\prime,\end{array} (5.8)

Voor de nieuwe ruimte-tijd coördinaten van de twee verschillende gebeurtenissen op die lijn geldt dan ook weer
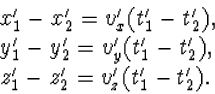
\begin{array} x_1^\prime-x_2^\prime=v_x^\prime(t_1^\prim... ...\prime-z_2^\prime=v_z^\prime(t_1^\prime-t_2^\prime).\end{array} (5.9)

Voor de absolute waarde v' van de snelheid $\vec v{\,}'$ kunnen we schrijven
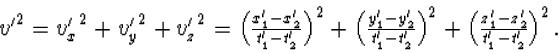
\begin{array} {v'}^2={v_x^\prime}^2+{v_y^\prime}^2+{v_z^... ...^\prime-z_2^\prime}{t_1^\prime-t_2^\prime}\right)^2.\end{array} (5.10)

We hebben aangenomen dat de lineaire transformatie de kwadratische vorm (5.1) en dus ook (5.6) invariant laat, d.w.z.
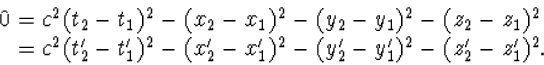\begin{array} 0=c^2(t_2-t_1)^2-(x_2-x_1)^2-(y_2-y_1)^2-(... ...y_2^\prime-y_1^\prime)^2-(z_2^\prime-z_1^\prime)^2.\end{array} (5.11)

Dit geeft
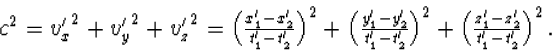
\begin{array} c^2={v_x^\prime}^2+{v_y^\prime}^2+{v_z^\pr... ...^\prime-z_2^\prime}{t_1^\prime-t_2^\prime}\right)^2.\end{array} (5.12)

en hieruit volgt v'2 =c2, of v'=c, hetgeen we wilden bewijzen.

Dit resultaat geeft ons de mogelijkheid om de transformaties die we in de relativiteitstheorie mogen gebruiken om inertiaalsystemen met elkaar te verbinden op een eenvoudige en algemene manier wiskundig te karakteriseren:

Een algemene Lorentz transformatie is een omkeerbare lineaire transformatie van de ruimte-tijd coördinaten die de kwadratische vorm c2t2-x2-y2-z2 invariant laat.

Deze transformaties, die we verder kortweg Lorentz transformaties zullen noemen, vormen een collectie die uiteraard de standaard Lorentz transformaties bevat en ook de zuiver ruimtelijke draaiingen zoals bijvoorbeeld de door formule (4.57) gegeven draaiingen om de z-as. Men kan laten zien dat iedere Lorentz transformatie in deze zin verkregen kan worden als resultaat van een eindig aantal elkaar opvolgende standaard Lorentz transformaties en ruimtelijke draaiingen.

We herhalen nog eens de formulering van het relativiteitsprincipe in de vorm die Einstein er aan gegeven heeft:

Alle inertiaalsystemen zijn fysisch equivalent: De natuurverschijnselen gedragen zich in ieder inertiaalsysteem op dezelfde manier. Verschillende inertiaalsystemen zijn met elkaar verbonden door Lorentz transformaties. De natuurwetten moeten daarom Lorentz-invariant zijn.

Tenslotte formuleren we een korte samenvattende conclusie en zeggen vast iets over wat verder besproken zal worden: De nieuwe interpretatie van Einstein van het relativiteitsprincipe, waarbij Lorentz transformaties zijn ingevoerd om overgangen tussen inertiaalsystemen te beschrijven, heeft er voor gezorgd dat het probleem van de constante lichtsnelheid is opgelost. Algemener blijkt te gelden dat de Maxwell theorie als geheel covariant is onder Lorentz transformaties. De Newtonse mechanica daarentegen is niet Lorentz covariant.

Omdat de Newtonse mechanica niet Lorentz-covariant is moet ze vervangen worden door een nieuw te formuleren mechanica. Ook dit is door Einstein gedaan. Het is experimenteel gebleken dat deze nieuwe mechanica de fysische realiteit nauwkeuriger beschrijft dan de mechanica van Newton, ook al blijft de laatste voor een groot gebied van fysiche verschijnselen een zeer goede benadering. We zullen de Einsteinse mechanica later in dit college bespreken, maar we willen eerst ingaan op enkele merkwaardige aspecten van de beschrijving van gebeurtenissen in de ruimte-tijd, zoals deze op eenvoudige manier uit de door Einstein gegeven gedachtengang volgt.

  • Volgende hoofdstuk
  • Naar inhoudsopave