Ruimte-tijd plaatjes

4.1 Ruimte-tijd plaatjes

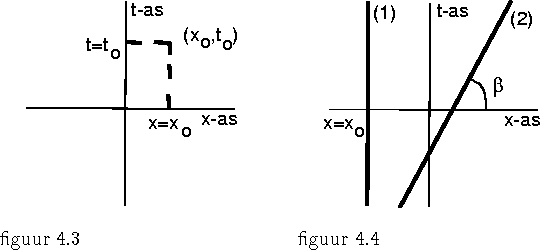
In een inertiaalsysteem wordt de 4-dimensionale ``ruimte-tijd'' opgesplitst in tijd en gewone ruimte; in verschillende inertiaalsystemen gebeurt dit op verschillende manieren en daardoor worden in de transformatieformules tussen inertiaalsystemen ruimte- en tijdcoördinaten gemengd. Om dit te begrijpen gaan we ruimte-tijd plaatjes tekenen. Het gaat ons om de relatie tussen tijd en ruimte, niet om de relatie tussen ruimtecoördinaten onderling. We kunnen daarom 2-dimensionale plaatjes gebruiken, met een t-as en één ruimtelijke as, bijvoorbeeld de x-as.

Een punt (x₀,t₀) in een plaatje als figuur 4.3 stelt een gebeurtenis voor. (De y- en z-coördinaten zijn natuurlijk niet getekend). Een lijn beschrijft de historie van een puntdeeltje. We noemen zo'n lijn een wereldlijn of levenslijn.

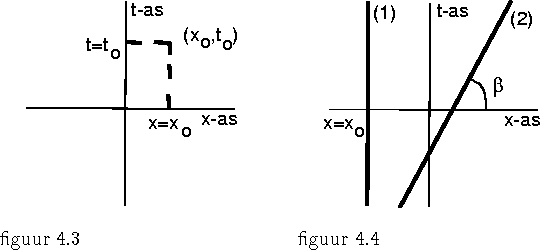
psfile=fig4-3en4.ps
figuur 4.3 -- figuur 4.4

We tekenen in figuur 4.4, 4.5 en 4.6 enkele wereldlijnen van op verschillende manier bewegende puntdeeltjes:

(1): Een deeltje in rust op x=x₀.
(2): Een eenparig rechlijnig bewegend deeltje met snelheid $v={\rm cotg} \beta$ . Het is duidelijk dat hoe kleiner de hoek $\beta$ is, hoe groter de snelheid is. Een horizontale lijn kan niet; dat zou een oneindige snelheid betekenen.
(3): Een tweetal deeltjes (bijvoorbeeld een electron en een positron) worden op t=t₀ gecreëerd en vliegen met tegengestelde snelheden weg.
(4): Een deeltje bevindt zich in rust op plaats x=x₀. Vanaf tijdstip t=0 ondervindt het een kracht waardoor het versneld gaat bewegen.
(5): Twee deeltjes passeren elkaar op t=t₀ en x=x₀.
(6): Twee deeltjes botsen op t=t₀ in x=x₀, hun snelheden keren om.

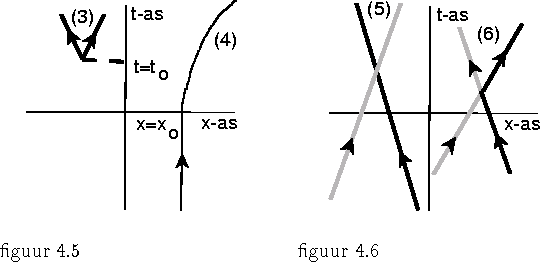
psfile=fig4-5en6.ps
figuur 4.5 -- figuur 4.6

Opgave 6:

Waarom is uit (6) in figuur 4.6 af te lezen dat de massa's van de twee deeltjes die met elkaar botsen gelijk moeten zijn.

Het is voor het nog volgende van groot belang zich te realiseren dat een 2-dimensonaal plaatje zoals hier getekend op de de eerste plaats gezien moet worden als een systeem van coördinaatlijnen die het 2-dimensionale vlak overdekken, zoals getekend in figuur 4.7. Denk daarbij aan grafiekpapier! De x-as is de lijn t=0, de t-as is de lijn x=0.

psfile=fig4-7en8.ps
figuur 4.7 -- figuur 4.8

Als volgende stap gaan we nu bekijken hoe coördinaattransformaties er in dergelijke 2-dimensionale ruimte-tijd plaatjes uitzien:

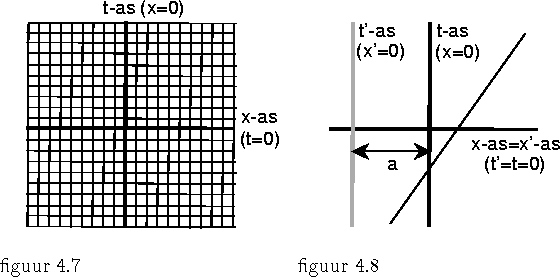
a. Eerst een zeer eenvoudig geval (figuur 4.8):

We verschuiven de oorsprong van het coördinaatsysteem over een afstand a. Op deze manier krijgen we op een zeer triviale manier uit het gegeven inertiaal systeem S een nieuw inertiaalsysteem S'. We hebben daarbij de transformatieformules
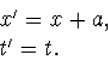$\begin{array} x'=x+a,\\ t'=t.\end{array}$ (4.3)

De t-as verschuift en de x-as blijft dezelfde. We moeten denken aan grafiekpapier: het zijn de x-lijnen die verschuiven. We zien uit het plaatje direct dat snelheden niet veranderen.

b. Nu een interessanter geval (figuur 4.9):

Bekijk een coördinaatsysteem S' dat zich ten opzichte van het gegeven stelsel S eenparig rechtlijnig beweegt, met snelheid u in de positieve x-richting. Het meest voor de hand liggend is dat de twee stelsels door een Galilei-transformatie verbonden zijn, dus door de formules
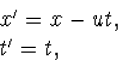$\begin{array} x'=x-ut,\\ t'=t,\end{array}$ (4.4)

Dit hebben we figuur 4.9 afgebeeld. De x-as en de x'-as liggen over elkaar heen; de t'-as is ten opzichte van de t-as gedraaid.

We moeten echter weer denken in termen van grafiekpapier: We zien dan dat de t-lijnen hetzelfde blijven, en dat de x-lijnen gedraaid zijn. We kunnen ook zien wat er met snelheden gebeurt: Een deeltje dat in S een snelheid v heeft, wordt in S' waargenomen als een deeltje met snelheid v-u, zoals we dat eerder besproken hebben. Dit is in overeen-stemming met de Newtonse mechanica, maar vanwege het constant zijn van de lichtsnelheid niet met de Maxwell theorie van het electromagnetisme.

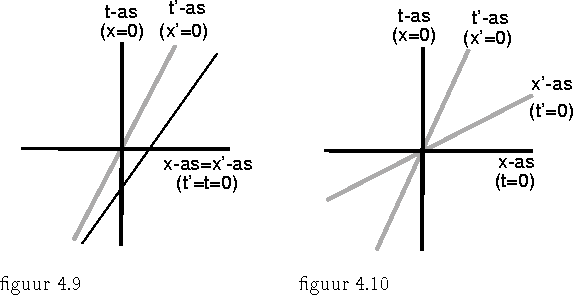
psfile=fig4-9en10.ps
figuur 4.9 -- figuur 4.10

c. We bekijken hetzelfde geval op een andere meer algemene manier (figuur 4.10):

We beginnen met een algemeen lineair verband tussen x, t en x', t' te veronderstellen:
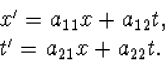
$\begin{array} x'=a_{11}x+a_{12}t,\\ t'=a_{21}x+a_{22}t.\end{array}$ (4.5)

De vier reële coëfficiënten a_jk vormen een $2\times 2$ matrix die we a noemen. De transformatie moet omkeerbaar zijn. Daarvoor moet de determinant van a ongelijk aan nul zijn. De inverse matrix is
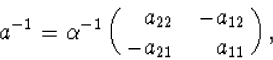$a^{-1}=\alpha^{-1}\pmatrix{\hphantom{-}a_{22}&-a_{12}\cr -a_{21}&\hphantom{-}a_{11}\cr},$ (4.6)

met $\alpha=\det a = a_{11}a_{22}-a_{12}a_{21}$ . De inverse transformatie heeft dan de vorm:
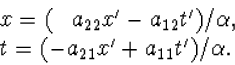$\begin{array} x=(\hphantom{-}a_{22}x'-a_{12}t')/\alpha,\\ t=(-a_{21}x'+a_{11}t')/\alpha.\end{array}$ (4.7)

De situatie die we willen beschrijven, een coördinaatstelsel S' dat zich ten opzichte van een gegeven stelsel met eenparige snelheid u beweegt, legt condities op aan de getallen a_jk. De wereldlijn van een punt dat in het stelsel S' vast is wordt beschreven door de vergelijking

x'=b', (4.8)

met b' constant. Omgerekend met formule (4.5) wordt dat in S

a₁₁x+a₁₂t=b', (4.9)

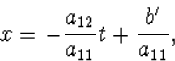$x=-\frac{a_{12}}{a_{11}}t+\frac{b'}{a_{11}},$

(4.10)

hetgeen betekent dat de snelheid van S' ten opzichte van S gelijk is aan -a₁₂/a₁₁. Dit moet u zijn, en dus hebben we a₁₂=-u a₁₁. Op dezelfde wijze gaan we uit van een vast punt in S met wereldlijn x=b. Omrekening naar S' met (4.7) geeft, als snelheid van S ten opzichte van S', a₁₂/a₂₂. Dit moet -u zijn en dus hebben we ook a₂₂=-a₁₂/u=a₁₁. De transformatie van S naar S' kunnen we daarmee schrijven als
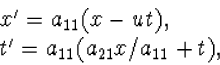$\begin{array} x'=a_{11}(x-ut),\\ t'=a_{11}(a_{21}x/a_{11}+t), \end{array}$ (4.11)

en de inverse transformatie van S' naar S als
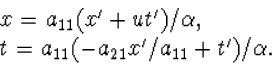$\begin{array} x=a_{11}(x'+ut')/\alpha,\\ t=a_{11}(-a_{21}x'/a_{11}+t')/\alpha.\end{array}$ (4.12)

Als we in deze formules a₂₁=0 en a₁₁=1 nemen, geldt t'=t en hebben we weer een Galilei transformatie terug gekregen. Dat willen we juist niet; we veronderstellen daarom dat $a_{21}\neq 0$ . We hebben daarmee een situatie zoals die in het ruimte-tijd plaatje van figuur 4.10 getekend is. We zien dat nu beide assen gedraaid zijn. In de zin van grafiekpapier zijn zowel de x-lijnen als de t-lijnen gedraaid. In de overgang van S naar S' zijn ruimte- en tijdmeting veel sterker door elkaar gemengd. Er geldt nog steeds dat rechte lijnen in rechte lijnen overgaan, dus eenparige bewegingen blijven eenparig. Snelheden veranderen echter op een manier die ingewikkelder is dan we kennen van het geval van de Galilei transformaties. Om dat te berekenen bekijken we een deeltje dat zich ten opzichte van S beweegt met snelheid v. De wereldlijn van het deeltje is een rechte lijn gegeven door de vergelijking

x(t)=vt+b. (4.13)

In S' wordt deze vergelijking, na enige herschrijving, en met gebruikmaking van de formules (4.12),

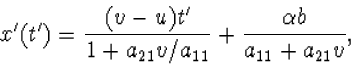
$x'(t')=\frac{(v-u)t'}{1+a_{21}v/a_{11}}+\frac{\alpha b}{a_{11}+a_{21}v},$

(4.14)

hetgeen betekent dat het deeltje in S' een snelheid v' heeft met
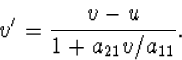$v'=\frac{v-u}{1+a_{21}v/a_{11}}.$ (4.15)

Voor a₂₁=0 zou dit weer de transformatieformule van snelheden onder een Galilei transformatie zijn. Daarbij zouden de snelheden eenvoudig optellen. In de algemene situatie is dat niet meer het geval. We kunnen nu wel de vrijheid, die we nog in de keuze van de a₂₁ en a₁₁ hebben, gebruiken om er voor te zorgen dat bij de transformaties één bepaalde snelheid niet verandert. Dat moet natuurlijk de lichtsnelheid c zijn. We hebben dan de vergelijking
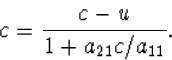$c=\frac{c-u}{1+a_{21}c/a_{11}}.$ (4.16)

waarmee we a₂₁ in a₁₁ kunnen uitdrukken. We vinden

a₂₁=-ua₁₁/c². (4.17)

De transformatieformules (4.11) worden daarmee

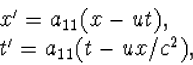
$\begin{array} x'=a_{11}(x-ut),\\ t'=a_{11}(t-ux/c^2),\end{array}$

(4.18)

en de inverse formules (4.12)
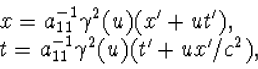$\begin{array} x=a_{11}^{-1}\gamma^2(u)(x'+ut'),\\ t=a_{11}^{-1}\gamma^2(u)(t'+ux'/c^2),\end{array}$ (4.19)

met daarbij
$\gamma(u)=1/\sqrt{1-u^2/c^2}.$ (4.20)

We kunnen de vrijheid in a₁₁ nog gebruiken om te zorgen dat (4.18) en (4.19), op het teken van u na, de zelfde vorm krijgen. Daartoe kiezen we $a_{11}=\gamma(u)$ . Daarmee hebben we tenslotte de transformatieformules
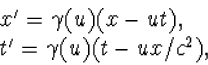$\begin{array} x'=\gamma(u)(x-ut),\\ t'=\gamma(u)(t-ux/c^2),\end{array}$ (4.21)

en de inverse formules
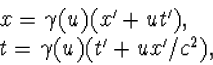
$\begin{array} x=\gamma(u)(x'+ut'),\\ t=\gamma(u)(t'+ux'/c^2),\end{array}$ (4.22)

Dit noemen we een Lorentz transformatie. (Dergelijke transformatieformules zijn voor het eerst voorgesteld door H.A. Lorentz, die er echter nog niet de juiste interpretatie voor had. Deze is pas door Einstein gegeven.)

Een kortere afleiding van de Lorentz transformatie gaat als volgt: De oorsprong in het stelsel S', weergegeven door x'=0, wordt in het stelsel S weergegeven door de eenparig rechtlijnige beweging x(t)=ut, oftewel x-ut=0. Omdat we willen dat de transformatie lineair is moet dus gelden dat $x'=\gamma(u)(x-ut)$ . Omgekeerd kunnen we uitgaan van de oorsprong in S, weergegeven door x=0, die in S' wordt beschreven door x'+ut'=0, zodat $x=\gamma(-u)(x'+ut')$ . Merk op dat de relativiteit ons oplegt dat de ene transformatie te verkrijgen is uit de andere door de snelheid van richting te laten omkeren. Maar we zijn volledig vrij de richting van positieve x-as te kiezen, omdat de ruimte isotroop is. (De ruimte-tijd is ook homogeen, hetgeen ons de vrijheid geeft het nulpunt van plaats en tijd te kiezen). Dus concluderen we dat $\gamma(u)=\gamma(-u)$ . We gebruiken nu dat een lichtstraal vanuit de oorsprong, op t=0 beginnende, in beide stelsels beschreven wordt door x=ct en x'=ct'. Enerzijds volgt daaruit dat $ct'=x'=\gamma(u)(ct-ut)=\gamma(u)(c-u)t$ , anderzijds, de rol van S en S' verwisselend, $ct=x=\gamma(u)(ct'+ut')=\gamma(u)(c+u)t'$ . Hieruit kunnen we $\gamma(u)$ oplossen, bijv. door de twee uitdrukking met elkaar te vermenigvuldigen en links en rechts t' t uit te delen. Men vindt eenvoudig dat $\gamma(u)=1/\sqrt{1-u^2/c^2}$ . Verder kunnen we ook t' in termen van x en t bepalen, door $x=\gamma(x'+ut')$ te schrijven als $t'=(x/\gamma-x')/u$ en vervolgens de uitdrukking $x'=\gamma(x-ut)$ te substitueren. Er volgt $t'=\gamma(t-ux/c^2)$ en de uitdrukking van t in termen van x' en t' wordt hieruit verkregen door u van teken om te laten klappen.

Deze afleiding van de Lorentz transformatie is minder abstract geformuleerd dan de vorige. Bovendien zal het symmetrieprincipe dat we geburikten vaker van pas komen.

Samenvattend:

Lorentz transformaties verbinden, net als Galilei transformaties, inertiaalsystemen op een manier die in overeenstemming is met het relativiteitsprincipe en het lichtpostulaat. In tegenstelling tot Galilei transformaties laten ze de lichtsnelheid invariant. Hiermee zijn ze in overeenstemming met de Maxwell theorie van het electromagnetisme.

We moeten hier wel een prijs voor betalen: Op de eerste plaats vinden we, zoals we eerder in het gedachtenexperiment met de kogel zagen, dat snelheden niet meer eenvoudig mogen worden opgeteld. Ook uit (4.15) krijgen we de transformatieformule voor snelheden
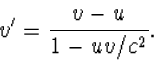$v'=\frac{v-u}{1-uv/c^2}.$ (4.23)

Een tweede daarmee samenhangend en nog veel belangrijker punt is dat de Newtonse mechanica niet meer invariant is onder Lorentz transformaties. We gaan dit in deze eenvoudige twee dimensionale situatie na.

Bezie een deeltje met willekeurige, d.w.z. niet noodzakelijk eenparige beweging. Zijn wereldlijn wordt in S gegeven door een functie x(t) en in S' door x'(t'). Het is handig om zo'n wereldlijn te zien als een kromme in de ruimte-tijd die los van mogelijke coördinaatsystemen beschreven wordt door een parameter $\tau$ . Een dergelijke parameter kan tamelijk willekeurig gekozen worden; de keuze heeft geen invloed op ons resultaat. Met zo'n parameter wordt de beweging weergegeven door functies f en g volgens
$x=f(\tau),\quad t=g(\tau).$ (4.24)

De snelheid van het deeltje is dan
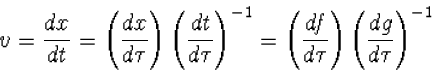$v=\frac{dx}{dt}=\left(\frac{dx}{d\tau}\right)\left(\frac{dt}... ...\left(\frac{df}{d\tau}\right)\left(\frac{dg}{d\tau}\right)^{-1}$ (4.25)

en de versnelling

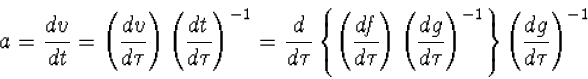
$a=\frac{dv}{dt}=\left(\frac{dv}{d\tau}\right)\left(\frac{dt}... ...g}{d\tau}\right)^{-1}\right\}\left(\frac{dg}{d\tau}\right)^{-1}$

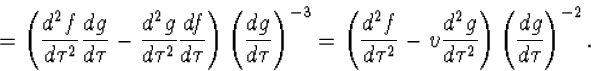$\qquad=\left(\frac{d^2f}{d\tau^2}\frac{dg}{d\tau}-\frac{d^2g... ...\frac{d^2g}{d\tau^2}\right)\left(\frac{dg}{d\tau} \right)^{-2}.$

(4.26)

In S' hebben we voor de beschrijving van het zelfde deeltje functies f' en g'
$x'=f'(\tau),\quad t'=g'(\tau).$ (4.27)

met daarbij
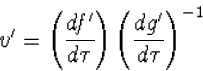
$v'=\left(\frac{df'}{d\tau}\right)\left(\frac{dg'}{d\tau}\right)^{-1}$ (4.28)

en ook
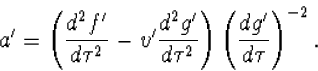$a'=\left(\frac{d^2f'}{d\tau^2}-v'\frac{d^2g'}{d\tau^2}\right) \left(\frac{dg'}{d\tau}\right)^{-2}.$ (4.29)

We drukken v' in v uit. We gebruiken (4.21)
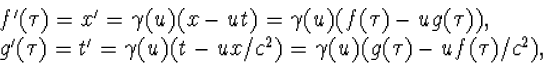
$\begin{array} f'(\tau)=x'=\gamma(u)(x-ut)=\gamma(u)(f(\t... ...\gamma(u)(t-ux/c^2)=\gamma(u)(g(\tau)-uf(\tau)/c^2),\end{array}$ (4.30)

en vervolgens
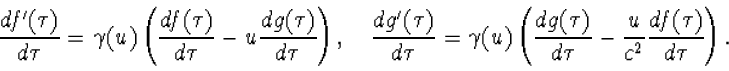$\begin{array}\frac{df'(\tau)}{d\tau}=\gamma(u)\left(\fr... ...}{d\tau}-\frac{u}{c^2}\frac{f(\tau)}{d\tau}\right).\end{array}$ (4.31)

Daarmee vinden we
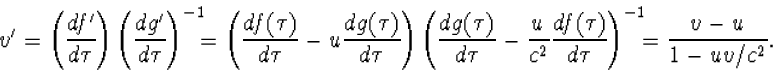
$\begin{array} v'=\left(\frac{df'}{d\tau}\right)\left(\f... ...c{f(\tau)}{d\tau}\right)^{-1}=\frac{v-u}{1-uv/c^2}.\end{array}$ (4.32)

Dit is formule (4.23), de transformatieformule voor snelheden, maar nu algemeen geldig voor deeltjes met willekeurige beweging. We drukken tenslotte a' uit in a en v. Om de afleiding doorzichtig te houden gebruiken we hier even de verkorte notatie
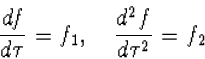$\frac{df}{d\tau}=f_1,\quad \frac{d^2f}{d\tau^2}=f_2$ (4.33)

en idem voor de afgeleiden van f', g en g'. Met deze notatie is de versnelling in S gelijk aan

a=(f₂g₁-f₁g₂)/g₁³. (4.34)

Met de relaties

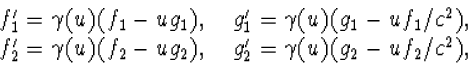
$\begin{array} f_1^\prime=\gamma(u)(f_1-ug_1),\quad g_1^\... ...(f_2-ug_2),\quad g_2^\prime=\gamma(u)(g_2-uf_2/c^2),\end{array}$

(4.35)

schrijven we de versnelling in S' als
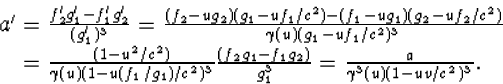$\begin{array} a'=\frac{f_2^\prime g_1^\prime-f_1^\prime ... ...-f_1g_2)}{g_1^3}=\frac{a}{\gamma^3(u)(1-uv/c^2)^3}.\end{array}$ (4.36)

Het uiteindelijke resultaat van deze tamelijk ingewikkelde berekening is eenvoudig. De keuze van de parameter $\tau$ loopt vooruit op de eigentijd die we later in zullen voeren. Een belangrijke vereenvoudiging wordt verkregen als we een andere keuze voor de parameter maken. Het meest voor de hand ligt om voor $\tau$ de tijd t in het stelsel S te gebruiken. Dus we beschrijven in het stelsel S een deeltje dat een willekeurige beweging x(t) ondergaat en als gewoonlijk definiëren we v(t)=dx(t)/dt en a(t)=dv(t)/dt, zijnde respectievelijk de snelheid en de versnelling. Door de Lorentz transformatie naar het stelsel S' uit te voeren, vinden we wat de baan van het deeltje in dat stelsel is geparametriseerd door de tijd t van het stelsel S (let op, niet als functie van t'). Uiteraard hebben we $x'(t)=\gamma(u)(x(t)-ut)$ en $t'(t)=\gamma(u)(t-ux(t)/c^2)$ . Hieruit zijn de snelheid v' en de versnelling a' in het stelsel S' te bepalen door gebruik te maken van de kettingregel voor het nemen van de t' afgeleide, v'=dx'/dt'=(dx'(t)/dt)/(dt'(t)/dt) en a'=dv'/dt'=(dv'(t)/dt)/(dt'(t)/dt).

Opgave 7:

Leidt nu zelf met bovenstaande de formules (4.32) en (4.36) af.

Het gaat hierbij om een versnelling die ieder moment in de richting van de snelheid u, de x-richting, plaats heeft. Het is zeker niet vanzelfsprekend dat dezelfde transformatie geldt voor een versnelling loodrecht op u. Hiertoe kiezen we nu in het stelsel S een beweging die beschreven wordt door y(t), zodat v_y=dy(t)/dt en a_y=dv_y(t)/dt, beide dus in de y-richting wijzende, hetgeen de reden is waarom we een index y gebruiken. Door transformatie naar het S' stelsel vinden we $\vec x{\,}'(t)=(-ut\gamma(u),y(t),0)$ en $t'(t)=t\gamma(u)$ .

Opgave 8:

Laat zien dat $\vec v{\,}'=(-u,v(t)/\gamma(u),0)$ en dat $\vec a{\,}'=(0,a(t)/\gamma^2(u),0)$ .

We zien dus dat de versnellingscomponent loodrecht op de richting van de snelheid u anders transformeert dan evenwijdig aan die richting!

Opgave 9:

Bewijs voor een deeltje met een versnelling zowel in de x als de y richting, dat $a^\prime_x=a_x\gamma^{-3}(u)(1-v_xu/c^2)^{-3}$ en dat $a^\prime_y=a_y\gamma^{-2}(u)(1-v_xu/c^2)^{-2}+uv_y a_xc^{-2}\gamma^{-2} (u)(1-v_xu/c^2)^{-3}$ en dat dit overeenstemt met de twee specifieke gevallen die we hebben beschreven.

Aan het resultaat voor de transformatie van de versnellingen kunnen we een duidelijke conclusie verbinden. Er geldt $a\neq a'$ , dus $ma\neq ma'$ . Als de beweging van het deeltje veroorzaakt wordt door een kracht F betekent dat men niet tegelijkertijd F=ma in S en F=ma' in S' kan hebben. Dus:

De vergelijking F = ma, de basisvergelijking van de Newtonse mechanica, is niet invariant onder Lorentz transformaties.

We vatten nu de voorafgaande twee dimensionale formules op als formules die betrekking hebben op een situatie in de gewone vier dimensionale ruimte-tijd, waarbij inertiaalsystemen S' zich ten opzichte van een gegeven systeem S in de richting van de x-as bewegen. We kunnen dan de Lorentz transformatie formules (4.21) direct uitbreiden tot 4-dimensionale formules
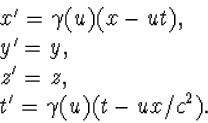$\begin{array} x'=\gamma(u)(x-ut),\\ y'=y,\\ z'=z,\\ t'=\gamma(u)(t-ux/c^2).\end{array}$ (4.37)

Dit zullen we de standaard Lorentz transformatie in de x-richting noemen. De inverse formules (4.22) worden natuurlijk aangevuld tot
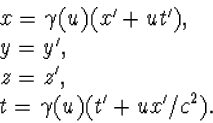$\begin{array} x=\gamma(u)(x'+ut'),\\ y=y',\\ z=z',\\ t=\gamma(u)(t'+ux'/c^2).\end{array}$ (4.38)

We hebben ook standaard Lorentz transformaties in de y-richting
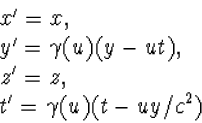$\begin{array} x'=x,\\ y'=\gamma(u)(y-ut),\\ z'=z,\\ t'=\gamma(u)(t-uy/c^2)\end{array}$ (4.39)

en standaard Lorentz transformaties in de z-richting
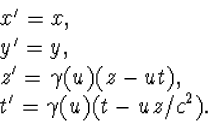$\begin{array} x'=x,\\ y'=y,\\ z'=\gamma(u)(z-ut),\\ t'=\gamma(u)(t-uz/c^2).\end{array}$ (4.40)

Tenslotte zijn er ook standaard Lorentz transformaties in een willekeurige richting. De formules hiervoor zijn natuurlijk wat ingewikkelder. We zullen ze niet afleiden, maar geven ze hier. Als het nieuwe systeem S' zich ten opzichte van S beweegt met een snelheid $\vec u=(u_x,u_y,u_z)$ wordt de transformatie van ruimte-tijd coördinaten gegeven door
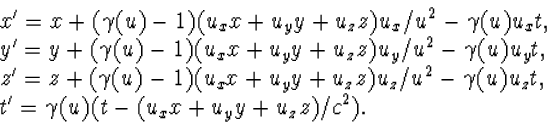
$\begin{array} x'=x+(\gamma(u)-1)(u_xx+u_yy+u_z z)u_x/u^2... ...amma(u)u_zt,\\ t'=\gamma(u)(t-(u_xx+u_yy+u_z z)/c^2).\end{array}$ (4.41)

Hierin is u²=u_x²+u_y²+u_z² en $\gamma(u)=(1-u^2/c^2)^{-{\scriptstyle{{1\over 2}}}}$ .

Opgave 10:

In vectornotatie (zie hoofdstuk 7 als U niet vertrouwd bent met deze notatie) luidt (4.41) $\vec x{\,}'=\vec x+(\gamma(u)-1)(\vec u\cdot\vec x)\vec u/u^2- \gamma(u)\vec u t$ en $t'=\gamma(u)(t-\vec u\cdot\vec x/c^2)$ . Laat zien dat de oorsprong van het stelsel S' beschreven wordt door de eenparig rechtlijnige beweging $\vec x=\vec u t$ en dat een lichtstraal uitgezonden in een willekeurige richting, beschreven door $\vec x=\vec c t$ (met $\vec c\cdot\vec c=c^2$ ) ook beschreven wordt door $\vec x{}'= \vec c{\,}' t'$ (met $\vec c{\,}'\cdot \vec c{\,}'=c^2$ ). Wat kunt U over de richting van de lichtstraal in het stelsel S' zeggen.

Opgave 11:

(i.) Ga na dat we de formules (4.37) voor de standaard Lorentz transformatie in de x-richting terug krijgen door in (4.41) u_x=u, u_y=u_z=0 te nemen.
(ii.) Ga uit van een inertiaalsysteem S met ruimte-tijd coördinaten x, y, z, t. Ga met een Lorentz transformatie naar een tweede inertiaalsysteem S' dat zich met een snelheid u₁ in de x-richting t.o.v. S beweegt. Bekijk vervolgens een derde inertiaalsysteem S'' dat zich t.o.v. S' met een snelheid u₂ in de x'-richting beweegt. Laat zien dat de rechtstreekse transformatie van de oorspronkelijke S naar deze laatste S'' weer een standaard Lorentz transformatie in de x-richting is, en leidt daaruit af dat S'' zich t.o.v. S beweegt met een snelheid u die gelijk is aan

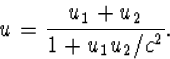$u=\frac{u_1+u_2}{1+u_1u_2/c^2}.$

(4.42)

Belangrijke algemene opmerking:

We zien in deze formule en ook in allerlei andere formules, zoals de formules voor Lorentz transformaties (4.20), (4.21), (4.22), (4.37), (4.38) etc., voor de transformaties van snelheden (4.23) en van versnellingen (4.36), factoren als u/c, u²/c² en uv/c². In veel situaties zijn deze factoren erg klein omdat de snelheden u en v erg klein zijn in vergelijking met de lichtsnelheid c.

Als illustratie bekijken we een numeriek voorbeeld bij formule (4.42): We gaan uit van een coördinaatstelsel S dat vast aan het aardoppervlak verbonden is. S' bevindt zich in een supersonisch vliegtuig dat een snelheid heeft van u=2700 km per uur en S'' is verbonden aan een raket die vanuit het vliegtuig naar voren wordt afgevuurd, met een snelheid u'= 3600 km per uur t.o.v. het vliegtuig. Volgens de relativiteitstheorie heeft dan de raket een door formule (4.42) bepaalde snelheid u'', die van de som u+u' afwijkt met ongeveer $8\times10^{-10}\%$ . Zelfs bij deze voor aardse omstandigheden hoge snelheden zal het buitengewoon moeilijk zijn om de relativistische afwijking van de Newtonse beschrijving te meten.

Conclusie:

In de limiet van snelheden die klein zijn ten opzichte van de lichtsnelheid gaan de formules van de Einsteinse relativiteitstheorie over in de formules van de Newtonse beschrijving. Dit betekent dat de Newtonse theorie waardevol blijft als een zeer goede benadering voor het grote gebied van fysische verschijnselen waarbij geen snelheden optreden die van de zelfde orde van grootte zijn als de lichtsnelheid.

Volgende paragraaf

Naar inhoudsopave