De relativiteitstheorie van Einstein is wellicht een van de meest tot de verbeelding sprekende theorieën uit de natuurwetenschappen, en

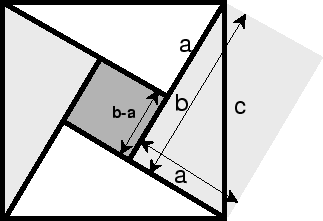
De stelling van Pythagoras is die andere formule die bijna iedereen kan opdreunen. Al is het natuurlijk niet de bedoeling af te dwalen naar de meer mystieke betekenis van het woord formule: ``geijkte uitdrukking bij zekere traditionele of ambtelijke handelingen'' (een ritueel, zoals de Engelsen het wat duidelijker omschrijven). Nee, een formule is niets anders dan een uitdrukking in de taal van de wiskunde, waarin iets zo precies mogelijk wordt gezegd. Voor de stelling van Pythagoras is dat: het kwadraat (c²) van de schuine zijde (c) is de som van de kwadraten (a²+b²) van de rechte zijden (a en b) van een rechthoekige driehoek. Of ook, de oppervlakte (c²) van een vierkant met zijden die even lang zijn als de schuine zijde (c), is de som van de oppervlakten (a²+b²) van de twee vierkanten ieder met de zijden gelijk in lengte aan een van de twee rechte zijden (a en b). En zo hebben we bijna een bewijs van de stelling van Pythagoras geleverd. Zie de figuur hieronder,

waar we het vierkant met oppervlak c² opbouwen uit de vier rechthoekige driehoeken, met schuine zijde c en rechte zijden a en b. Daarbij houden we een vierkantje over, waarvan de zijden een lengte b-a hebben. Omdat twee dezelfde rechthoekige driehoeken, met hun schuine zijden tegen elkaar, een rechthoek geven met zijden a en b en dus met een oppervlak a X b geldt dat (c²) gelijk is aan twee maal dat oppervlak (2ab, of ook vier maal het oppervlak van de driehoek), plus het oppervlak van het overblijvende vierkantje ((a-b)²). Nu wat simpele algebra:

Wat we ons altijd bij formules moeten realiseren is dat de symbolen in het algemeen abstract zijn. De schuine zijde noemen we hier c, maar alleen in speciale gevallen bedoelen we daar inderdaad de lichtsnelheid mee. Met ons bewijs via oppervlakten is c, evenals a en b, natuurlijk een lengte. Toch kunnen we de stelling van Pythagoras ook toepassen als het over snelheden gaat. Stel namelijk dat we een snelheid in een bepaalde richting ontbinden in een horizontale en een vertikale snelheid. D.w.z. dat het object, waarvan we de snelheid meten, in 1 seconde a meter in de horizontale richting beweegt en tegelijkertijd b meter in de vertikale richting. De vraag is nu, wat is de totale afstand die het object in die ene seconde heeft afgelegd? Dat is natuurlijk de lengte van de schuine zijde van de driehoek met rechte zijden a en b meter. Maar nu kunnen we onze oppervlakte-afleiding¹ van de stelling van Pythagoras gebruiken om te concluderen dat de lengte van de schuine zijde gelijk is aan

meter,

We kunnen nu makkelijk een situatie beschouwen waarbij c inderdaad de lichtsnelheid is. Daarvoor sturen we licht onder een bepaalde hoek met de horizontale richting omhoog, en ontbinden de beweging van het licht in een horizontale en vertikale richting. De weg die het licht in één seconde aflegt is echter voor menselijke maatstaven gigantisch groot, namelijk driehonderd duizend kilometer, of wel driehonderd miljoen meter (als we heel precies willen zijn geldt c=299.793 km/s). Het is in zo'n geval beter voor de tijd kleinere eenheden te nemen, zoals de milliseconde (éénduizendste seconde) of nog beter de microseconde, éénmiljoenste seconde. In 1 microseconde beweegt het licht nog steeds ongeveer 300 meter. Eigenlijk is de zogenaamde nanoseconde (éénmiljardste seconde) meer geschikt. In deze tijd legt het licht een afstand van 30 cm af. Dit maakt ook duidelijk dat de lichtsnelheid heel groot is in vergelijking met de snelheden waaraan de mens, zelfs in deze jachtige tijd, gewend is. Zo is de snelheid van het geluid ca. 330 m/s (dit noemt men ook wel Mach 1) al groot, maar valt in het niets ten opzichte van de snelheid waarmee de aarde om de zon beweegt, 30 km/s. Maar zelfs deze snelheid is nog steeds een factor tienduizend kleiner dan de lichtsnelheid. Bedenk dat dit zich verhoudt als de snelheid van een slak (10 m/h) tot die van een auto (100 km/h).

Dit is de reden waarom we in het dagelijks leven zo weinig rechtstreeks van de relativeitstheorie van Einstein merken, en nog belangrijker, waarom het zo moeilijk voor ons is ons te verplaatsen naar een wereld waar de snelheden wél groot zijn en de effecten die Einstein voorspeld heeft wél makkelijk waarneembaar zijn. Einstein's uitgangspunten waren de volgende waarnemingsfeiten, geformuleerd in de drie postulaten van de relativiteitstheorie.

• Relativiteitsprincipe: Natuurkundige wetten zijn in alle stelsels (coördinaten en klok waarmee iemand zijn waarnemingen doet) hetzelfde.
• Lichtpostulaat: De lichtsnelheid in het luchtledige is in ieder intertiaal stelsel (een stelsel waar geen krachten op werken) hetzelfde.
• Equivalentieprincipe: In vrije val bewegen alle objecten met dezelfde versnelling.

Het lichtpostulaat is in feite een gevolg van een veel vroegere theorie, namelijk die van Maxwell. Hij bracht de electriciteit en het magnetisme in één theorie samen, het electromagnetisme. Maxwell liet zien hoe licht een electromagnetische golf is, waarbij afwisselend het magnetische veld verandert, daarbij een veranderend electrisch veld veroorzaakt, dat op zijn beurt weer een veranderend magnetisch veld genereert, enz. Uit de theorie van Maxwell volgde al dat de voortplantingssnelheid van het licht niet afhangt van de bewegingstoestand van de waarnemer, noch van de bewegingstoestand van de bron. Het zat er echter zo ingehamerd bij de natuurkundigen van de negentiende eeuw, dat golven zich door een medium voortplanten, en dat de beweging van de waarnemer ten opzichte van het medium opgeteld moet worden bij die van de golf in het medium, dat het lang geduurd heeft voordat het als zodanig werd onderkend. Daar was Einstein voor nodig.

Laten we maar meteen onze kennis over de stelling van Pythagoras gebruiken om aan te tonen dat uit het lichtpostulaat volgt dat we een bewegende klok langzamer zien lopen dan een stilstaande klok. Een klok is een mechanische constructie die twee opeenvolgende tijdstippen vastlegt, hetzij door de wijzers van de klok, cijfers op een display, of door ieder ander natuurkundig verschijnsel dat zich telkens herhaalt. Omdat het lichtpostulaat iets over licht zegt, nemen we als uitgangspunt de zg. lichtklok. Bij deze klok kaatst licht heen en weer tussen twee spiegels. Dat licht wordt uitgezonden met een zeer korte pulsduur, zodat we daarvan het begin nauwkeurig kunnen bepalen en hiermee het tijdsverschil tussen twee opeenvolgende tikken van de klok kunnen aflezen. We kiezen voor deze tijdsduur tussen twee tikken één nanoseconde waarin het licht heen en weer gaat. In die tijd legt het licht 30 centimeter af, dus staan de spiegels op een afstand van L=15 centimeter. We kiezen deze eenheid van een nanoseconde voor de duur tussen twee tijdstikken om een handzame klok te verkrijgen. De relatie tussen de tijdsduur en de afstand geldt uiteraard alleen als de klok stilstaat ten opzichte van ons, als waarnemer. Hou de klok nu rechtop, dus de spiegels evenwijdig aan de grond, maar laat de gehele klok bewegen met een snelheid v. Als we mee zouden reizen met de klok verandert er natuurlijk niets, maar wij blijven stil staan en volgen het licht van onder naar boven en weer terug. Omdat de spiegels met een snelheid v bewegen, hebben deze tussen de tijd van het vertrek van het licht en de aankomst bij de bovenste spiegel een afstand vT/2 afgelegd, en nog eens dezelfde afstand op de terugweg, zie de figuur. Hierbij is T uiteraard de tijdsduur voor het op en neer gaan van het licht, maar gezien vanuit onze waarnemingspositie. Om deze tijd T te bepalen, rekenen we uit wat de afstand is die het licht heeft afgelegd. Hier komt de stelling van Pythagoras mooi van pas, want deze afstand is twee maal de lengte van de schuine zijde van de rechthoekige driehoek die we in de figuur hebben aangegeven. De verticale rechte zijde heeft een lengte L, en de horizontale rechte zijde een lengte vT/2. Dus de weg die het licht heeft afgelegd is gelijk aan

.

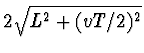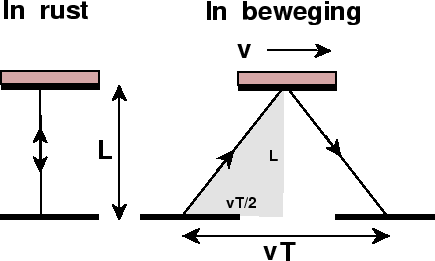
Nu komt het lichtpostulaat van pas, want die snelheid is dus gelijk aan c (onafhankelijk van de beweging van de klok, die met een constante snelheid beweegt, zodat er - in goede benadering - geen krachten op werken). Dus

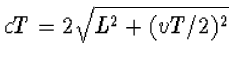
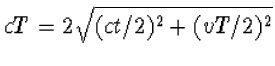
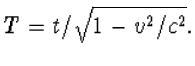
U zult gemerkt hebben dat we telkens het waarnemingsaspect benadrukken. En waarnemen gaat nu eenmaal meestal via licht. Het was ook de eigenschap van het licht die aanleiding gaf tot dit, op het eerste gezicht, bizarre resultaat. Waarom is dit de meeste mensen nooit opgevallen.² Dat komt omdat in de dagelijkse praktijk de snelheden zo klein zijn ten opzichte van de snelheid van het licht. Laten we de omloopsnelheid van de aarde om de zon als voorbeeld nemen. Daarvoor is dus v/c=1/10000. Bij het berekenen van de tijdsdilatatie moeten we hiervan het kwadraat nemen. De afwijking in de gang van de klok is bij deze snelheid slechts 1 op 200 miljard seconden, of 1 seconde in 6 jaar, 4 maanden en 2 dagen. Dat kan men met atoomklokken wel meten, maar maakt echter wel duidelijk dat we er in het dagelijkse leven niets van merken. Toch zult U ongetwijfeld denken dat het komt door de manier waarop we de tijd hebben gemeten. Echter, laten we eens een heel andere klok nemen. Denk aan een koekoeksklok, een digitale klok, of wat mij betreft een tennisklok, waar een tennisbal op en neer stuitert (dan moeten we wel aannemen dat er geen energie verloren gaat bij het stuiteren, of door de wrijving met de lucht, maar het idee is duidelijk). Als we deze klokken in rust met elkaar vergelijken kunnen we bepalen hoeveel tikken de lichtklok heeft, binnen één tik van de koekoeks-, tennis- of digitale klok (dat zullen veel tikken zijn, maar dat maakt niet uit). Als nu al die klokken ten opzicht van ons bewegen, dan staan ze nog steeds stil ten opzicht van elkaar, en lopen dus nog steeds gelijk, ook voor ons, omdat het eenduidig is wanneer op dezelfde plaats en dezelfde tijd twee tikken samenvallen. Hoe raar het op het eerste gezicht ook lijkt, de tijdsdilatie is een universeel verschijnsel, en wordt daarbij van een eigenschap die bewegende klokken hebben, verheven tot een eigenschap van de tijd.

Een consequentie van het lichtpostulaat is dus dat er iets vreemds met de tijd gebeurt. Dit volgt ook uit het beroemde gedachtenexperiment van Einstein met een trein. We kunnen daarmee illustreren dat gelijktijdigheid van gebeurtenissen op vershillende punten in de ruimte afhangt van de bewegingstoestand van de waarnemer. Immers als we midden in de trein tegelijkertijd vanaf hetzelfde punt naar links en rechts een lichtpuls versturen, dan komt deze voor de waarnemer in de trein tegelijkertijd aan de voor en de achterkant van de trein aan. Maar als we nu diezelfde gebeurtenis vanaf het perron waarnemen, dan is de achterkant van de rijdende trein wat in de richting van de lichtbron verschoven tijdens de reis van de lichtpuls, terwijl de voorkant van de trein juist wat verder weg is gegaan. De puls zal dus eerder aan de achterkant arriveren dan aan de voorkant. Dit is zo, omdat ook voor de waarnemer op het perron de snelheid van het licht gelijk is aan c.

Met een tijd die langer wordt voor bewegende klokken, maar een snelheid die onafhankelijk van de beweging is, ligt het voor de hand dat de waargenomen lengte van een meetlat korter wordt. Dit is de beroemde Lorentzcontractie, vernoemd naar de Leidse hoogleraar die zijn naam heeft gegeven aan het Instituut voor Theoretisch Natuurkunde. We geven de bewegende klok een lampje mee dat gedurende de tijd T aan is. We nemen nu een meetlat met een lengte L₀, waarlangs de klok beweegt, precies zo dat het lampje alleen aan is zolang de klok zich ter hoogte van de meetlat bevindt. Dus L₀=vT. Hoe ziet dit eruit voor iemand die met de klok meebeweegt, en ten opzichte waarvan de meetlat dus beweegt met een snelheid v? Voor die waarnemer is het lampje aan gedurende een tijd

.

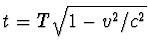
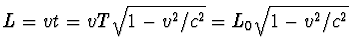We zien dat de bewegingstoestand een belangrijk rol speelt. Helaas wordt vaak het begrip ``alles is relatief'' uit zijn verband gerukt, en vaak buiten de natuurkunde toegepast. Maar ook binnen de natuurkunde kan dit tot grote verwarring aanleiding geven. We gaan nu, om U in die verwarring te brengen, de beroemde tweelingenparadox bespreken.³ We sturen een astronaut met een snelheid die achttiende van de lichtsnelheid bedraagt (v=0,8 c) naar de ster alpha Centauri, die op ongeveer een afstand van 4 lichtjaar staat. In de sterrenkunde zijn alle afstanden groot, en om te voorkomen dat we over de grote getallen struikelen hebben de sterrenkundigen de grootheid lichtjaar ingevoerd. Dit is de afstand die het licht in één jaar aflegt. Dus 300.000 km/s maal 365 (=aantal dagen in een jaar) maal 24 (=aantal uren in een dag) maal 3600 s (=aantal seconden in een uur), ofwel ongeveer 9,5 triljard kilometer (9,5 X 10¹² km). Om U een idee te geven, de afstand van de aarde tot de zon is ca. 8,3 lichtminuten.

De tweelingbroer van de astronaut blijft achter op aarde. Gemeten op zijn klok doet de astronaut over de 4 lichtjaren slechts 5 aardse jaren. Immers het licht doet er 4 jaar over en de snelheid van de astonaut is 8/10, ofwel 4/5, van die van het licht. De astronaut doet er een factor 5/4 langer over dan het licht, dus 5 jaar. Als we even aannemen dat de astronaut meteen terugreist met dezelfde snelheid, dan doet hij er nog eens 5 aardse jaren over om terug te komen. Dus na 10 aardse jaren is de astronaut weer veilig terug. Maar nu hebben we een probleem. Voor de astronaut wordt zijn leeftijd bepaald door een klok die met hem meereist. Het levensritme, waarmee ademhaling, celdeling en sterfte plaatshebben is zo'n (weliswaar niet bijster nauwkeurige) klok. Omdat deze klok beweegt ten opzichte van de tweelingbroer weet ook hij dat de klok van de astronaut minder snel loopt, en wel met een factor

.

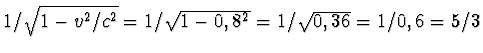Waarom geeft dit zoveel verwarring? De foute redenering zegt dat volgens Einstein alles relatief is, de natuurwetten zijn in ieder stelsel gelijk. Dus kunnen we ook doen alsof de astronaut op zijn plaats blijft en de tweelingbroer over 4 lichtjaren heen en weer reist, en dus jonger terug zou moeten komen. Maar hij kan niet én jonger én ouder zijn. Maar laten we even iets preciezer zijn. Het is niet zo dat we bij de omkering van de rol van astronaut en tweelingbroer de laatste over 4 lichtjaren heen en weer sturen, nee we moeten met hem de hele aarde, ja zelfs het hele zonnestelsel, de melkweg, het hele heelal over 4 lichtjaar heen en weer sturen. En geloof me, er is geen raket in het universum die zoveel stuwkracht kan geven dat we dit allemaal voor elkaar krijgen. Door de versnelling en de vertraging die nodig zijn om de astronaut zijn snelheid te geven, kan men niet de rol van astronaut en tweelingbroer verwisselen. Het zijn zowel de versnellingen als de vertragingen die in feite de astronaut zijn verjonging opleveren. Hardlopers zijn in dit geval dus geen doodlopers!

Men heeft deze verjongingskeur echt kunnen meten, door met gevoelige atoomklokken een vliegreis te maken. Ook in de grote deeltjesversnellers, waar electrisch geladen deeltjes met snelheden dicht bij die van het licht worden rondgestuurd, en waar dus het effect van de tijdsdilatatie erg groot is, heeft men het effect ondubbelzinnig aangetoond. Het is zelfs zo dat de deeltjesversnellers niet eens kunnen werken zonder hiermee rekening te houden. In ons voorbeeld hoort de snelheid van 0,8 c natuurlijk nog lang niet tot de mogelijkheden van de aardse ruimtevaart (maar wel van de deeltjesfysica). Echter, met de populaire serie Star Trek is het tegenwoordig wat minder moeilijk een voorstelling te maken van wat het betekent om met zulke grote snelheden te reizen.

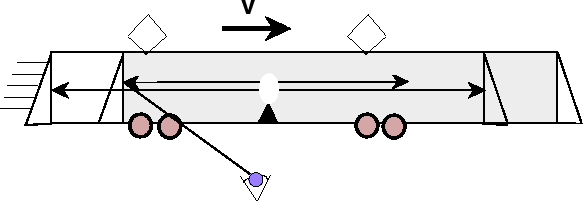
Einstein heeft bij het ontwikkelen van zijn theorie veel gebruik gemaakt van gedachtenexperimenten. Één daarvan hebben we al besproken. In Einstein's tijd waren die vaak niet praktisch uitvoerbaar. Vóórdat we nog een voorbeeld van een gedachtenexperiment van Einstein bespreken, noem ik een erg fraai resultaat dat kan worden verkregen door een gedachtenexperiment dat David Mermin heeft verzonnen. Dit laat zien dat uit het lichtpostulaat volgt dat, bijvoorbeeld een kogel die met een snelheid v binnen een trein wordt afgevuurd in de richting van de beweging van de trein (welke met een snelheid u aan het perron voorbij rijdt) ten opzichte van dat perron niet een snelheid u+v heeft, maar een snelheid

Hoewel voor Mermin's afleiding van het ``optellen'' van snelheden geen ingewikkelde algebra nodig is, zou het toch te ver voeren het hier helemaal door te rekenen. Ik maak U er met bovenstaande figuur warm voor, te proberen het zelf te berekenen. Het fraaie idee van Mermin was dat we op twee manieren kunnen uitrekenen op welke fractie f van de totale lengte van de trein een kogel en lichtpuls elkaar ontmoeten, als deze tegelijk vanaf de achterkant werden afgevuurd.⁴ Namelijk één keer vanuit het oogpunt van iemand die veilig op het perron achterblijft

Nu komen we dan eindelijk toe aan E=mc². Ook hiervoor gebruikte Einstein fraaie gedachtenexperimenten. We hebben daarbij het begrip ``hoeveelheid beweging'' nodig (ook wel impuls genoemd). Dat is massa vermenigvuldigd met snelheid, of mv. Het blijkt zo te zijn dat de totale hoeveelheid beweging behouden is als er op het geheel waarvan we deze totale hoeveelheid beweging bepalen geen uitwendige krachten werken. Dit verklaart de terugstoot bij het afvuren van een geweer. De kogel gaat in voorwaartse richting, het geweer in achterwaartse richting. De massa van de kogel is veel kleiner dan die van het geweer, waardoor de terugslag van het geweer evenredig veel kleiner is. Hetzelfde bij de voortstuwing van een raket: Die gaat vooruit door de verbrandingsgassen die naar achteren worden gestuwd. Ook de botsing van biljartballen wordt door het behoud van de hoeveelheid beweging (én van energie) bepaald. Schieten we een biljartbal precies in het midden op een andere biljartbal, dan valt de bal die we stoten stil en gaat de geraakte bal met de snelheid van de gestote bal verder. De hoeveelheid beweging is behouden, want beide biljartballen hebben dezelfde massa.⁶

Het behoud van de hoeveelheid beweging is volledig equivalent met de opmerking dat het zwaartepunt van een systeem waarop geen uitwendige krachten werken niet versnelt. Als het zwaartepunt beweegt dan kunnen we onze metingen in het stelsel doen waarin het zwaartepunt in rust is. De coördinaten van het zwaartepunt worden in dit zogenaamde rust- of zwaartepuntstelsel bepaald door de coördinaten van ieder object, vermenigvuldigd met de massa van dat object, bij elkaar op te tellen en te delen door de totale massa. Een tijdje later zijn de coördinaten veranderd maar blijft het zwaartepunt hetzelfde. Omdat de componenten van de snelheid in de verschillende coördinaatrichtingen worden bepaald door de verandering van de coördinaten te delen door de tijd, zien we aldus dat de totale hoeveelheid beweging niet verandert (in het zwaartepuntstelsel is de totale hoeveelheid beweging gelijk aan nul). Daarnaast is het natuurlijk iedereen bekend dat de totale energie altijd behouden moet zijn. Beide wetten zijn op de ervaringswereld gebaseerd, maar hebben ook een diepere betekenis die samenhangt met het feit dat er (althans in principe) in de ruimte geen voorkeurspunt en in de tijd geen voorkeurstijd is aan te geven. Hierover heeft Prof. Icke U in de eerste lezing al heel wat fraais verteld.

We hebben nog één ingrediënt nodig, namelijk dat licht naast een hoeveelheid energie, ook een hoeveelheid beweging heeft. Dit is de zogenaamde stralingsdruk en deze is niet zo eenvoudig te meten, maar heeft onder andere (deels) te maken met het feit dat kometen een staart vormen, en de zon niet onder zijn eigen gewicht instort. Beide eigenschappen volgen ook uit de theorie van Maxwell. Daaruit volgt tevens dat de energie van het licht precies gelijk is aan de hoeveelheid beweging vermenigvuldigd met de snelheid c. Einstein's beroemde formule laat zien dat de energie van het licht equivalent is met een hoeveelheid massa. Gewoonlijk bepalen we massa door op een weegschaal objecten met elkaar te vergelijken. Daarbij wordt zo'n object, bijvoorbeeld een appel, eerst stil gelegd op de weegschaal en dan gewogen. Dit heet ook wel rustmassa. Maar licht kan niet stil gezet worden. Dat is de ultieme consequentie van het lichtpostulaat. Het beweegt altijd met de snelheid c. Als we het toch stilzetten, kan het geen energie meer hebben, maar uitspraken doen over niets heeft weinig zin. We zeggen wel dat licht een rustmassa gelijk aan nul heeft. Toch blijkt uit het volgende gedachtenexperiment van Einstein dat de energie van het licht wel degelijk bijdraagt aan massa. Einstein liet dit zien door naar het zwaartepunt van een doos te kijken, waarbij binnen de doos een lichtpuls wordt uitgestuurd. Doordat deze puls een hoeveelheid beweging heeft, zal de doos een terugstoot ondervinden. De doos beweegt dan in de tegengestelde richting, totdat de lichtpuls aan de andere kant van de doos wordt opgevangen. Hierbij draagt het precies de juiste hoeveelheid van beweging aan de doos over, om deze weer tot stilstand te brengen. Maar terwijl het licht van de ene kant naar de andere kant is bewogen, heeft de doos een afstand afgelegd, die weliswaar klein is (omdat de lichtsnelheid zo groot is), maar niet gelijk aan nul. Echter al die tijd hebben er geen krachten van buiten op de doos gewerkt. Het zwaartepunt moet daarom op zijn plaats blijven. Dat kan alleen als de lichtpuls de hoeveelheid beweging van de doos neutraliseert. Maar dat betekent dat de lichtpuls een massa vertegenwoordigt, want anders zou het niet aan het de hoeveelheid beweging kunnen bijdragen.

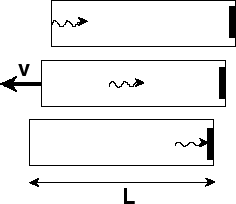
Het is niet moeilijk om uit te rekenen wat deze equivalente massa is. Als E de energie van de lichtpuls is, dan is de hoeveelheid beweging dus E/c. Als het licht, zoals in bovenstaande figuur, naar rechts beweegt krijgt de doos een terugslag (met snelheid v) naar links, met een hoeveelheid beweging Mv die gelijk is aan E/c. De massa van de doos is M, maar de waarde daarvan is niet van belang. Het licht legt een afstand L af gedurende de tijd t=L/c, terwijl de doos in die tijd een afstand d=vt aflegt. Nadat het licht aan de rechterwand is geabsorbeerd komt de doos weer tot stilstand en heeft het zwaartepunt zich dus verplaatst over een afstand⁷ mL-Md. Hierbij is m de massa die het licht nodig heeft om dit zwaartepunt op zijn plaats te houden, zodat dus mL-Md=0 een oplossing heeft. We vullen nu eerst in dat d=vt, dan t=L/c, en tenslotte Mv=E/c. We vinden daarmee

Als een deeltje wel een rustmassa (m₀) heeft, dan is het nu ook duidelijk dat de massa van de snelheid af moet hangen. Want als een deeltje een snelheid krijgt, dan wint het aan energie.⁸ Deze bewegingsenergie is gelijk aan E_k=m₀v²/2, de zogenaamde kinetische energie, maar dit geldt alleen bij lage snelheden. De totale energie is dan de energie bij rust, ofwel de rustenergie E₀=m₀c², plus de kinetische energie. Dus

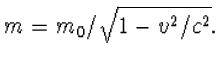
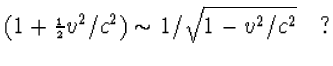
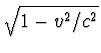
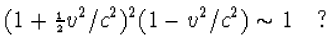
Nu begrijpt U ook waarom niets sneller dan het licht kan. Hoe groter de snelheid is, hoe groter de massa, hoe moeilijker het wordt nog meer snelheid te maken. Als v=c wordt de massa oneindig groot en kost het oneindig veel moeite om de snelheid op te voeren. Hiervoor is het natuurlijk essentieel dat de formule voor de snelheidsafhankelijke massa inderdaad juist is. Geen nood. Nog één mooi gedachtenexperiment en ik heb U ook daarvan overtuigd.

We nemen twee klitteballen, bolletjes die blijven kleven als ze tegen elkaar aan worden gegooid, ieder met precies dezelfde rustmassa m₀. We doen dit door ze precies met dezelfde snelheid v, maar in exact tegengestelde richting, te laten botsen. Omdat de massa's gelijk zijn (hoewel in beweging m ongelijk m₀ is), komen ze exact tot rust na de botsing (behoud van hoeveelheid beweging). Dit heet een inelastische botsing, in tegenstelling tot een elastische botsing bij biljartballen. De twee klitteballen vormen nu een geheel, en we noemen de rustmassa van dat geheel M₀. We gaan nu precies dezelfde botsing bekijken vanuit het stelsel dat meebeweegt met één van de klitteballen voor de botsing, maar daarna met de snelheid v blijft bewegen. In dit nieuwe stelsel heeft de andere klittebal vóór de botsing een snelheid w (en een massa m'), die we krijgen door v relativistisch op te tellen bij v.

We willen nu laten zien dat

In het oorspronkelijke stelsel hebben we het behoud van hoeveelheid beweging al gebruikt om te concluderen dat de samenklittende klitteballen stilvallen. Maar behoud van energie vertelt ons dat M₀c² gelijk aan de energie moet zijn die vóór de botsing in de twee klitteballen zat. Ieder heeft een energie

,

.

We bespreken tot slot nog kort wat consequenties van het laatste postulaat: in vrije val ondervindt alles dezelfde versnelling. Dit is de reden waarom in een ruimtestation dat om de aarde cirkelt er gewichtsloosheid heerst. Alles valt namelijk met dezelfde versnelling naar de aarde. Door precies de juiste baansnelheid te kiezen blijft het ruimteschip echter in zijn continue valbeweging op dezelfde hoogte boven het aardoppervlak. Nog een andere manier om dit postulaat te formuleren is dat versnelling equivalent is met gravitatie. Ook dit kent U uit de dagelijkse ervaring. Een optrekkende lift geeft U het idee zwaarder te zijn (het experiment met een vrijvallende lift is niet aan te bevelen). We kunnen zo'n kunstmatig gravitatieveld maken door een roterend wiel als ruimtestation te maken, wellicht hét ontwerp voor een permanent ruimtestation voor de volgende generatie. Door de rotatie ontstaat een centrifugale druk op de buitenwand van het roterende ruimtestation, en bij de juiste omloopsnelheid kunnen we het makkelijk zo inrichten dat we letterlijk de aarde onder onze voeten voelen. De omloopsnelheid geeft aanleiding tot een tijdsdilatatie van de klokken op de roterende wand ten opzichte van een klok die in het midden stilstaat. Daar waar de klok stilstaat heerst géén centrifugale kracht. Op de wand hoort bij de kracht een ontsnappingsnelheid. Voor een roterende beweging is de onsnappingsnelheid (v_ont) precies gelijk aan de omloopsnelheid. Klokken in het centrifugale krachtenveld lopen dus langzamer met een factor

.

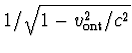We concluderen dus, en wonderlijk genoeg is dit precies goed, dat klokken in een gravitatieveld langzamer lopen met een factor gegeven door

.

.

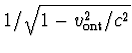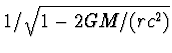Opmerkelijk genoeg komt de tijd stil te staan op een afstand r=2GM/c². Dit heet de Schwarzschildstraal. Voor de zon is deze straal 2,95 km (en voor de aarde 0,9 cm), maar dat geldt alleen als alle massa is samengeperst binnen deze afstand. De Schwarzschildstraal is uiteraard ook de afstand waar de ontsnappingsnelheid gelijk is aan de lichtsnelheid. Licht kan dus niet vanuit een straal die kleiner is dan de Schwarzschildstraal naar buiten komen. Het wordt een zwarte ster, zoals Laplace zich al realiseerde. Echter met de algemene relativiteitstheorie van Einstein komt daar ook de tijd stil te staan, en wordt deze Schwarzschildstraal tot een gat in de ruimte-tijd. Vandaar de naam ``ZWART GAT''.

Hopelijk heb ik met bovenstaande mijn doel bereikt deze fraaie theorie ook voor niet ingewijden van haar mystiek te ontdoen. Formules waren er niet ter bezwering van het onbekende, maar ter verduidelijking van het bekende. De algebra is simpel, de consequentie echter verstrekkend. Dat is ook juist de aantrekkingskracht van deze theorie. Ik hoop ook dat U iets meekrijgt van de ``schoonheid'' van de natuurkunde. Ik heb er geen enkel probleem mee hierover vaag te blijven. Het is net als met muziek, een kwestie van smaak. Mooie theorieën hebben, net als mooie muziek, meer kans op eeuwige roem, maar laten ons ook steeds beter de natuur begrijpen. Het blijft opmerkelijk en wonderlijk hoe effectief onze wiskundige beschrijving van de natuur met de werkelijkheid overeenkomt, evenals de harmonieleer ons aangeeft welke frequentieverhouding lekker in het gehoor ligt.

Tot slot wil ik U op twee prachtig geschreven boeken over dit onderwerp wijzen. ``Mr. Tompkins in Paperback'', door George Gamow (Cambridge University Press, 1965) en ``Einstein's Mirror'', door Tony Hey en Patrick Walters (Cambridge University Press, 1997).