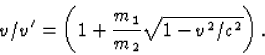- 6.
- a/b.
 en
en 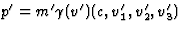 , met v'2=v'12+v'22+
v'32. Volgens de relativistische versie van energie-impuls behoud geldt
nu p'=p1+p2, zodat
, met v'2=v'12+v'22+
v'32. Volgens de relativistische versie van energie-impuls behoud geldt
nu p'=p1+p2, zodat
| 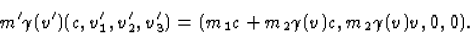 |
(23) |
Hieruit lezen we direct af dat v'2=v'3=0, en dus geldt v'=v'1.
- c.
- Uit p'2=m'2c2 (per definitie) volgt
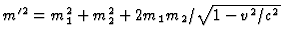 .
De x component van vgl. (23) geeft
.
De x component van vgl. (23) geeft 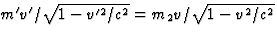 . Door dit te kwadrateren kunnen we
een vergelijking voor v'2 afleiden, (m22(v2/c2)/(1-v2/c2)+m'2)v'2
=m22v2/(1-v2/c2), waarin we de uitdrukking voor m'2 invullen. Dit
geeft na worteltrekken en herschikken,
. Door dit te kwadrateren kunnen we
een vergelijking voor v'2 afleiden, (m22(v2/c2)/(1-v2/c2)+m'2)v'2
=m22v2/(1-v2/c2), waarin we de uitdrukking voor m'2 invullen. Dit
geeft na worteltrekken en herschikken,
| 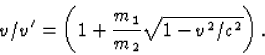 |
(24) |
- d.
- Als m1=m2 hangt v' niet van de massa's af.
 en
en 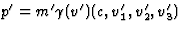 , met v'2=v'12+v'22+
v'32. Volgens de relativistische versie van energie-impuls behoud geldt
nu p'=p1+p2, zodat
, met v'2=v'12+v'22+
v'32. Volgens de relativistische versie van energie-impuls behoud geldt
nu p'=p1+p2, zodat
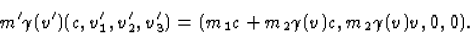
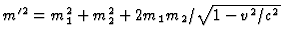 .
De x component van vgl. (23) geeft
.
De x component van vgl. (23) geeft 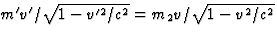 . Door dit te kwadrateren kunnen we
een vergelijking voor v'2 afleiden, (m22(v2/c2)/(1-v2/c2)+m'2)v'2
=m22v2/(1-v2/c2), waarin we de uitdrukking voor m'2 invullen. Dit
geeft na worteltrekken en herschikken,
. Door dit te kwadrateren kunnen we
een vergelijking voor v'2 afleiden, (m22(v2/c2)/(1-v2/c2)+m'2)v'2
=m22v2/(1-v2/c2), waarin we de uitdrukking voor m'2 invullen. Dit
geeft na worteltrekken en herschikken,