- a.
- Een deel van de bij het verval vrijkomende energie komt ten goede aan de
kinetische energie van het uitzendende deeltje, dat t.g.v impuls behoud een
terugslag krijgt bij de emissie. Dit komt in mindering op de energie van het
uitgezonden foton.
We stellen weer een impulsbalans op. Vóór de emissie hebben we
Na de emissie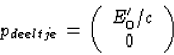
(32)
Wegens impuls behoud pdeeltje=p'deeltje+pfoton geldt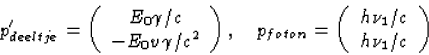
(33)
Uit het ruimtelijk deel van vgl. (34),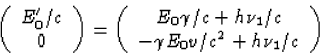
(34) 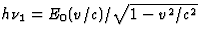 ,
volgt
,
volgt
Hieruit lossen we v op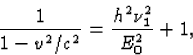
(35) 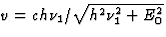 .Uit de tijdcomponent van vgl. (34) volgt dan (via vgl. (35))
.Uit de tijdcomponent van vgl. (34) volgt dan (via vgl. (35))
Substitutie van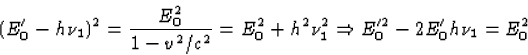
(36) 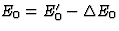 levert tenslotte
levert tenslotte
Zichtbaar licht heeft energieën van enkele eV en wordt uitgezonden door niet al te zware atomen. Als voorbeeld nemen we een natriumlamp (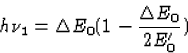
(37) 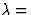 589
nm), fotonenergie 2 eV, massa Na-atoom 22 GeV, de verhouding is dan
589
nm), fotonenergie 2 eV, massa Na-atoom 22 GeV, de verhouding is dan 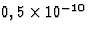 . Voor gammastraling (bijvoorbeeld zoals genoemd in (d) voor
Hg), is de energie 412 keV en de massa van de Hg kern is ongeveer 200 GeV.
In dat geval is de verhouding 10-6.
. Voor gammastraling (bijvoorbeeld zoals genoemd in (d) voor
Hg), is de energie 412 keV en de massa van de Hg kern is ongeveer 200 GeV.
In dat geval is de verhouding 10-6.
- b.
- In dit geval vangt het deeltje behalve de energie van het foton ook diens
impuls op. Het deeltje krijgt dus kinetische energie, die opgebracht moet
worden door de energie van het foton. Wil het foton ook een overgang kunnen
bewerkstelligen, dan zal het tengevolge van dit effect ook een iets hogere
energie moeten hebben. De impulsbalans is nu:
Voor de absorptie:
Na de absorptie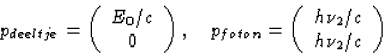
(38)
Wegens impuls behoud p'deeltje=pdeeltje+pfoton geldt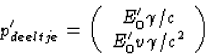
(39)
Uit het ruimtelijk deel van vgl. (40) leiden we af dat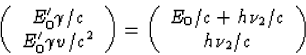
(40) 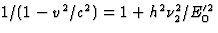 . Het tijdachtig deel geeft hiermee
. Het tijdachtig deel geeft hiermee 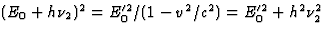 , zodat
, zodat 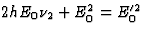 . We substitueren
hierin
. We substitueren
hierin 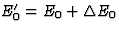 om te komen tot
om te komen tot
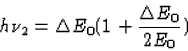
(41) - c.
- In een gas, i.h.b. bij hoge temperaturen, hebben de deeltjes een snelheid, alle kanten op. Dit geeft extra Doppler-effecten, zowel bij emissie als absorptie. Wannneer een absorberend deeltje en een uitzendend deeltje relatief naar elkaar toe bewegen, kan toch resonante absorptie optreden: immers, het absorberende deeltje ziet een hogere frequentie en energie t.g.v het Doppler effect. Dit kan compenseren voor het effect bij (a) en (b), die er beide voor zouden zorgen dat de frequentie van het uitgezonden foton te laag is om geabsorbeerd te kunnen worden. Een tweede effect is de natuurlijke lijnbreedte, dit is een quantummechanisch effect, t.g.v. de eindige levensduur van de aangeslagen toestand is er een onbepaaldheid in de energie, die de emissie- en absorptielijnen verbreedt.
- d.
- Bij het Mössbauer effect wordt de impuls niet overgedragen aan een enkel
deeltje, maar aan het hele kristal waarin de deeltjes gebonden zitten. T.g.v.
de grote massa van het kristal t.ov. de massa van een enkel deeltje treden
effecten bij (a) en (b) dus nu niet - of veel minder - op. De E0 en
E'0 in vgl. (37) en vgl. (41) moeten nu vervangen worden door de massa
van een heel kristal, grofweg 1023 maal zo veel. Derhalve geldt nagenoeg
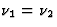 . De natuurlijke lijnbreedte in aanmerking nemende van de
overgangen, concluderen we dat de emissie en absorptielijnen nu wel voldoende
overlappen om resonante absorptie mogelijk te maken. Voorwaarde is wel dat het
kristal hecht genoeg is, d.w.z. dat de impuls van het foton niet zo groot is
dat roostertrillingen (z.g. fononen) aangeslagen kunnen worden.
. De natuurlijke lijnbreedte in aanmerking nemende van de
overgangen, concluderen we dat de emissie en absorptielijnen nu wel voldoende
overlappen om resonante absorptie mogelijk te maken. Voorwaarde is wel dat het
kristal hecht genoeg is, d.w.z. dat de impuls van het foton niet zo groot is
dat roostertrillingen (z.g. fononen) aangeslagen kunnen worden.
De vervolgvraag heeft niets met het Mössbauer effect te maken. Voor het Doppler-effect geldt
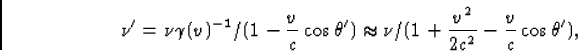
(42) waarbij
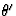 de hoek is tussen bewegingsrichting en signaalrichting,
waargenomen door de waarnemer (
de hoek is tussen bewegingsrichting en signaalrichting,
waargenomen door de waarnemer (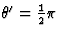 komt dan overeen met het
transversale Doppler-effect). Een radioactieve bron Hg wordt op het uiteinde
van een rotor geplaatst, de straling ervan wordt opgevangen met een
stilstaande detector. Deze bestaat uit een hoeveelheid vloeibaar kwik, met
een telbuis ernaast. Het detector-kwik gaat zelf stralen als het absorbeert.
Deze straling wordt gedetecteerd. Deze is maximaal als het kwik maximaal
absorbeert, m.a.w. als geldt dat de van de rotor afkomstige straling, verlaagd
t.g.v. de terugstoot bij emissie (onderdeel (a)) en verhoogd t.g.v. het
Doppler-effect, precies overeenkomt met de voor absorptie noodzakelijke
(onderdeel (b)) frequentie. We willen dus dat
komt dan overeen met het
transversale Doppler-effect). Een radioactieve bron Hg wordt op het uiteinde
van een rotor geplaatst, de straling ervan wordt opgevangen met een
stilstaande detector. Deze bestaat uit een hoeveelheid vloeibaar kwik, met
een telbuis ernaast. Het detector-kwik gaat zelf stralen als het absorbeert.
Deze straling wordt gedetecteerd. Deze is maximaal als het kwik maximaal
absorbeert, m.a.w. als geldt dat de van de rotor afkomstige straling, verlaagd
t.g.v. de terugstoot bij emissie (onderdeel (a)) en verhoogd t.g.v. het
Doppler-effect, precies overeenkomt met de voor absorptie noodzakelijke
(onderdeel (b)) frequentie. We willen dus dat 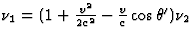 . Hieruit volgt
. Hieruit volgt
Voor het beschreven geval geldt
(43)  . Voor het zuiver longitudinale effect (
. Voor het zuiver longitudinale effect ( ) vinden we
dan v=665 ms-1. Voor een volledig transversaal effect (
) vinden we
dan v=665 ms-1. Voor een volledig transversaal effect ( )
zouden we moeten hebben
)
zouden we moeten hebben 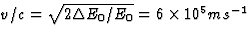 .
Dit is voor praktische doeleinden volstrekt onhaalbaar.
.
Dit is voor praktische doeleinden volstrekt onhaalbaar.