- 12.
- a.
- De relativistisch kinetische energie definiëren als Trel=Erel
-E0, waarbij
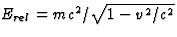 de nulcomponent is van de
energie-impulsviervector en E0 = m c2 de relativistische rustenergie. Deze
grootheid heeft de juiste klassieke limiet
de nulcomponent is van de
energie-impulsviervector en E0 = m c2 de relativistische rustenergie. Deze
grootheid heeft de juiste klassieke limiet 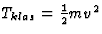 als
als 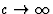 . Dit blijkt uit de expansie van Erel in v/c
. Dit blijkt uit de expansie van Erel in v/c
| 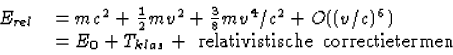 |
(25) |
Hieruit volgt
| 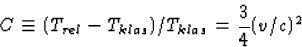 |
(26) |
Ook vinden we
| 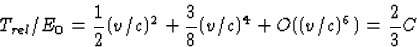 |
(27) |
Als 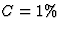 is Trel/E0=0,0066. (Ook Tklas/E0=0,0066, de
relativistische en klassieke kinetische energie zijn nagenoeg gelijk in dit
geval.)
is Trel/E0=0,0066. (Ook Tklas/E0=0,0066, de
relativistische en klassieke kinetische energie zijn nagenoeg gelijk in dit
geval.)
- b.
- Uit vgl. (26) volgt
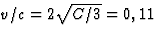 .
. - c.
- Uit vgl. (27) vinden we voor de toegestane kinetische energie
voor het electron
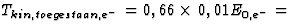 3,4
keV, voor het proton
3,4
keV, voor het proton 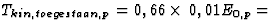 6,25 MeV
6,25 MeV
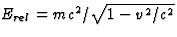 de nulcomponent is van de
energie-impulsviervector en E0 = m c2 de relativistische rustenergie. Deze
grootheid heeft de juiste klassieke limiet
de nulcomponent is van de
energie-impulsviervector en E0 = m c2 de relativistische rustenergie. Deze
grootheid heeft de juiste klassieke limiet 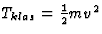 als
als 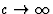 . Dit blijkt uit de expansie van Erel in v/c
. Dit blijkt uit de expansie van Erel in v/c
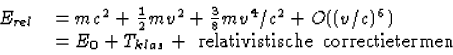
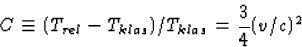
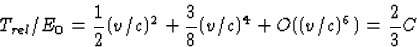
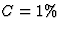 is Trel/E0=0,0066. (Ook Tklas/E0=0,0066, de
relativistische en klassieke kinetische energie zijn nagenoeg gelijk in dit
geval.)
is Trel/E0=0,0066. (Ook Tklas/E0=0,0066, de
relativistische en klassieke kinetische energie zijn nagenoeg gelijk in dit
geval.)
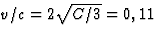 .
.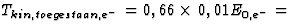 3,4
keV, voor het proton
3,4
keV, voor het proton 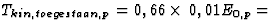 6,25 MeV
6,25 MeV