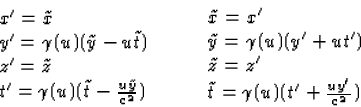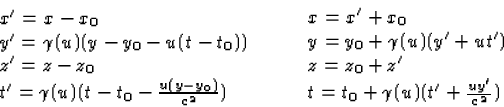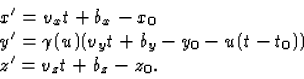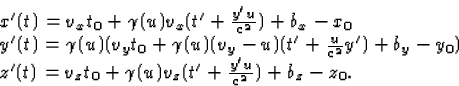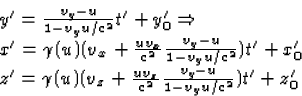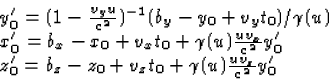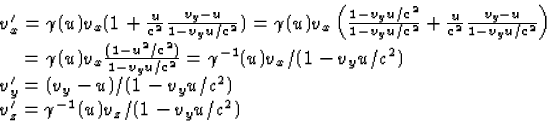- 1.
- De situatie in deze opgave verschilt van het standaard geval in de zin dat op
t = t' = 0 de oorsprong van S nu niet met die van S' samenvalt.
- a.
- Om de formules voor de Lorentz transformatie uit het standaardgeval
toe te kunnen passen, kiezen we hulpcoördinaten in S,
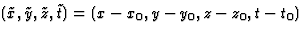 , zodat dit wel het geval is.
We gebruiken nu de formules (4.39) en het analogon van formule (4.38) voor
Lorentz transformaties in de y-richting:
, zodat dit wel het geval is.
We gebruiken nu de formules (4.39) en het analogon van formule (4.38) voor
Lorentz transformaties in de y-richting:
| 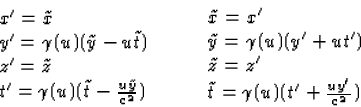 |
(1) |
In termen van de (x,y,z,t) wordt dit
| 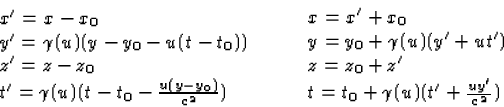 |
(2) |
- b.
- i.
- Om de formules van deze beweging t.o.v. S' te vinden, voeren we de Lorentz transformatie van vgl. (2) uit. Zo krijgen we uitdrukkingen voor (x',y',z') in termen
van (x(t),y(t),z(t)), ofwel (x'(t),y'(t),z'(t))
| 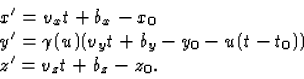 |
(3) |
De inverse Lorentz transformatie levert een uitdrukking voor t in termen van t' en y'.
Dit invullen in de uitdrukking voor (x'(t),y'(t),z'(t)) geeft:
| 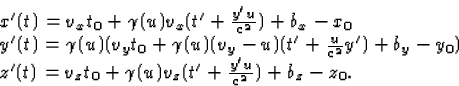 |
(4) |
We willen de y' afhankelijkheid elimineren om (x'(t'),y'(t'),z'(t')) te
krijgen. Dit doen we door uit de middelste vergelijking y' op te lossen als
functie van alleen t' en dit in de andere twee vergelijkingen in te vullen.
Zo komen we tot
| 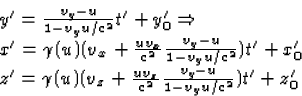 |
(5) |
met
| 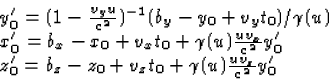 |
(6) |
- ii.
- De snelheden in S' zijn nu eenvoudig uit vgl. (5) af te lezen
| 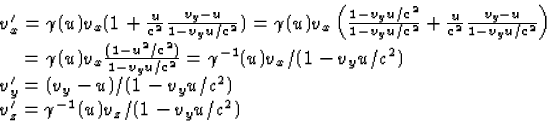 |
(7) |
Vergelijk dit met opg. 9 uit de syllabus, met de rollen van de x en y
richting omgedraaid. Het bepalen van relatieve snelheden gaat veel eenvoudiger
door gebruik te maken van de kettingregel, zoals in opg. 7-9 van de syllabus.
Hier hebben we door expliciete berekening ter controle laten zien
dat een eenparig rechtlijnige beweging in S, evenzo beschreven wordt als een
eenparige rechtlijnige beweging in S'.
- iii.
- eenvoudig invullen vx=vz=0 geeft v'x=0, v'y=(vy-u)/(1-
vyu/c2), v'z =0, precies het resultaat in vgl. (4.23) voor beweging in
de y-richting.
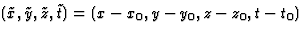 , zodat dit wel het geval is.
We gebruiken nu de formules (4.39) en het analogon van formule (4.38) voor
Lorentz transformaties in de y-richting:
, zodat dit wel het geval is.
We gebruiken nu de formules (4.39) en het analogon van formule (4.38) voor
Lorentz transformaties in de y-richting: