“Topological band insulators (TBI’s) are bulk insulators characterized by symmetry protected topological order. A while ago this was subject of an intense theoretical research effort in Leiden executed by Vladimir Juricic, Andrei Mesaros and especially Robert-Jan Slager who earned the exceptional cum laude honor for his thesis work. Presently this research is on stand-by waiting for experimental developments.
The result with the highest impact is the paper introducing the classification of TBI on basis of the space groups [192] Turn this into direct link to the papers themselves. This is generally regarded as the seminal paper introducing the basic notion while in the mean-time a large literature has emerged further refining this classification method. However, a central theme of our research was all along in the identification of the “bulk defects” associated with the topological order, playing a central role in our classification scheme. Although promising spectacular physics, these have been until recently completely ignored by the large community working on TBI’s, it seems for no other reason than that these require some out of the box thinking.
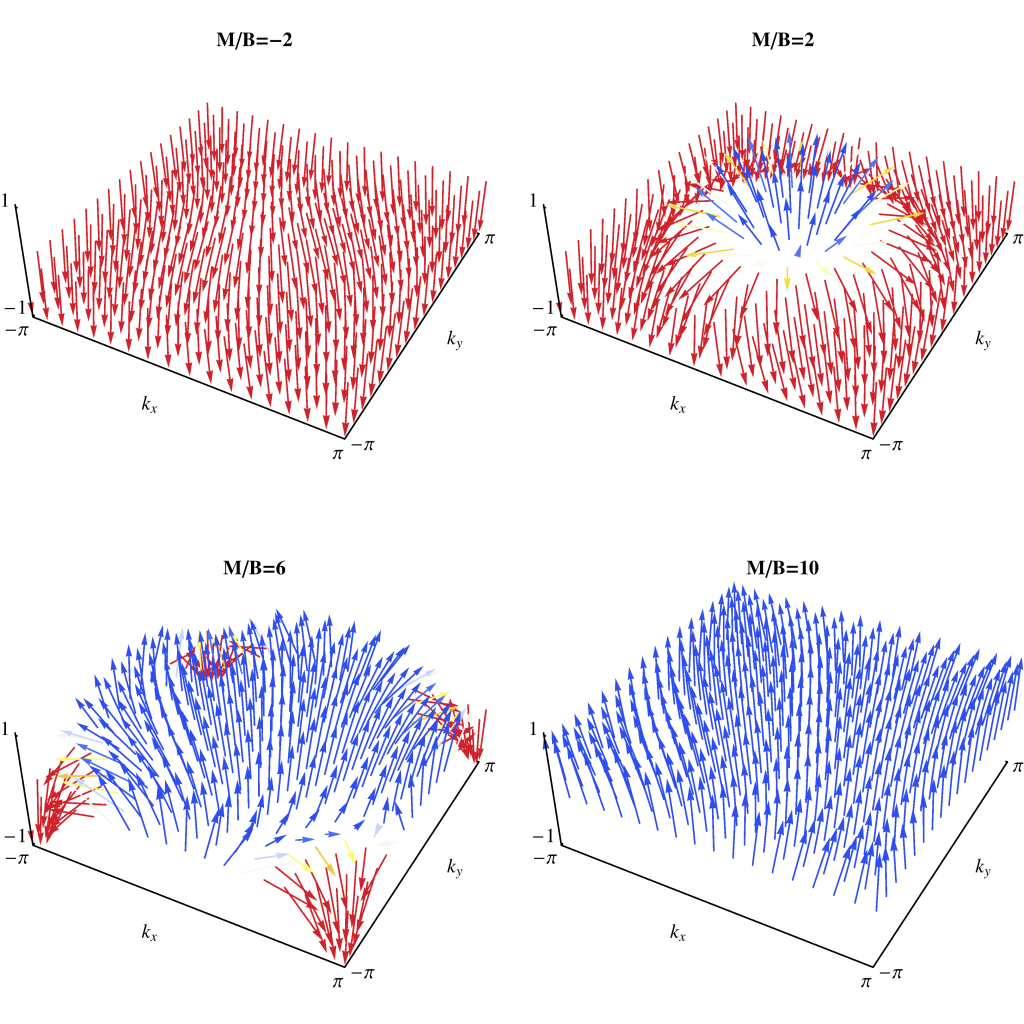
The role of dislocations and π fluxes can explicitly be shown within the context of the tight-binding M-B model on a square lattice , describing HgTe/CdTe quantum wells. As function of the parameter M/B the model has two topologically distinct nontrivial phases. For 0 < M/B < 4, the system exhibits a Γ phase with the bandgap located at zero momentum in the Brillouin zone. On the other hand, when 4 < M/B < 8 the band gap is located at finite momentum (M phase). This can be visualized by the presence of Skyrmions; the non-trivial phases display a full Skyrmion in the Brillouin zone, the position of which is at Γ or (π, π) respectively.
Dislocations are the work role. These take the role of magnetic flux in the quantum Hall effects. In the subclass of “translationally active” TBI’s electronic zero-modes bind to the dislocations [185, 193] and we showed early on that these are the literal incarnations of the Jackiw-Rossi zero modes: the 2 dimensional incarnations of the famous Su-Schrieffer-Heeger solitons representing the birth place of “electronic” topology. Among others, the resulting “spinon” and “holon” excitations exhibit a mutual Chern-Simons braiding statistics.
This becomes to full flourish in the three dimensional translationally active TBI’s. The zero modes spread in helical 1D modes propagating on the dislocation lines. These are similar as the edge modes in 2D in the sense that the electrons are “unstoppable”. Pending the details of the topological order it may well happen that the electronic conductance on these “perfect wires” becomes completely insensitive to the form and even motion of the dislocation lines [212]. A particular interesting case is realized on grain boundaries: these can be seen as arrays of dislocation lines and the 2D metal “topological metal” formed on the grain boundaries have most peculiar properties [220].
Figure 2: Grain-boundary semimetal localized on a 2D grain boundary in a translationally active 3D topological band insulator (the R phase of the BHZ model on a cubic lattice; see Appendix pp1 for details). (a) Schematic illustration of the 2D GB, which now realizes a sheet of parallel 1D edge dislocation lines that extend along the grain boundary. Each edge dislocation hosts a pair of propagating helical modes localized along the dislocation cores that cross at kz=π . (b) On a GB of opening angle 18.4∘ , the hybridization of the helical modes results in the semimetal band structure with two anisotropic pseudo-relativistic fermions at (kx,kz)=(0,π) and (π/d,π) . Along the GB we recover the same midgap bowtie dispersion as in the 2D case (shown top right for kz=π ), while along the edge dislocations the hybridized modes (orange) still flow into the bulk bands (gray) as a function of kz (bottom right for kx=π/d ). The data are for a 60×60×90 system with periodic boundary conditions
We suspect a whole world of new physics associated with these “perfect metal” dislocations, merging electromagnetism and elasticity/plasticity in a novel wholeness. In the mean time some first experimental attempts have been undertaken to detect these while we are eagerly awaiting a concerted experimental effort aimed at getting this spectacular potential under control in the laboratory.
