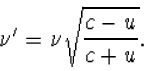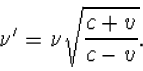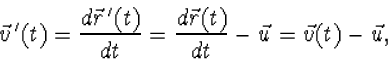Correcties Syllabus SRT - druk: Voorjaar 1999

Correcties voor de syllabus SRT - druk: Voorjaar 1999

-

Op pag. 8, in verg. (3.10) en (3.11) hadden natuurlijk vermeld moeten worden snelheid en versnelling in S', verkregen door respectivelijk de eerste en tweede afgeleide naar de tijd van verg.(3.9) te nemen.

$\begin{displaymath}\vec v{\,}'(t)=\frac{d\vec r{\,}'(t)}{dt}=\frac{d\vec r(t)}{dt}-\vec u= \vec v(t)-\vec u,\end{displaymath}$

(3.10)

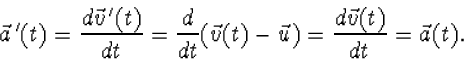$\begin{displaymath}\vec a{\,}'(t)=\frac{d\vec v{\,}'(t)}{dt}=\frac{d}{dt}(\vec v(t)-\vec u)= \frac{d\vec v(t)}{dt}=\vec a(t).\end{displaymath}$

(3.11)

-

Op pag. 11, in de 1e regel van opg. 3 is de kracht een factor $4\pi$ te klein. Er had moeten staan: $F_s=\mu_oq_1v_1q_2v_2/(4\pi r_{12}^2)$ .

-

Op pag. 12, 8e regel van onder: de stroomsnelheid is uiteraard 3 m/s (i.p.v. 5 km/s) en (twee regels daaronder) de snelheid van de speedboat is 5 m/s (i.p.v. 5 km/s).

-

Op pag. 12, 1e en 5e regel van boven: v=0,998 c (i.p.v. 0,966 c).

-

Op pag. 17, in fig. 4.2 moet de richting van u worden omgedraaid.
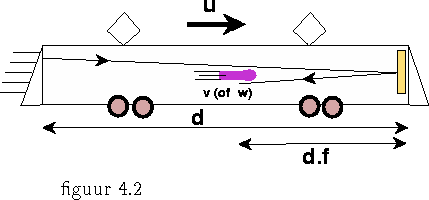
$\begin{figure} \vspace{3.3cm} \hskip4cm \special{psfile=mermin.ps voffset=-15 ho... ...le=55.0 hscale=55.0} \begin{center}figuur 4.2\end{center}\vskip-4mm \end{figure}$
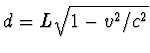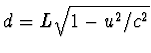Hoewel, zoals vermeld, de waarde van d zelf niet relevant is, zou de waarde die in de syllabus wordt gegeven, $d=L\sqrt{1-v^2/c^2}$ , niet de meest voor de hand liggende keuze zijn (dit is de lengte als gemeten in het stelsel waar de kogel in rust is). Waarschijnlijk bent U meer geneigd $d=L\sqrt{1-u^2/c^2}$ te nemen, relevant voor een waarnemer buiten de trein.

-

Op pag. 22, in verg. (4.19) worden links van de gelijkheid uiteraard x en t bedoeld (en niet x' en t').

$\begin{displaymath}\begin{array}{l} x=a_{11}^{-1}\gamma^2(u)(x'+ut'),\\ t=a_{11}^{-1}\gamma^2(u)(t'+ux'/c^2), \end{array}\end{displaymath}$

(4.19)

-

Op pag. 24, in verg. (4.31) en (4.32) zijn de d van de afgeleiden twee maal weggevallen, er had moeten staan:

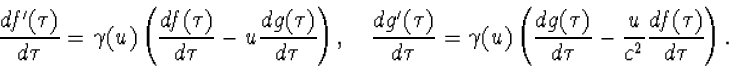$\begin{displaymath}\frac{df'(\tau)}{d\tau}=\gamma(u)\left(\frac{df(\tau)}{d\tau}... ...{dg(\tau)}{d\tau}-\frac{u}{c^2} \frac{df(\tau)}{d\tau}\right). \end{displaymath}$

(4.31)

Daarmee vinden we

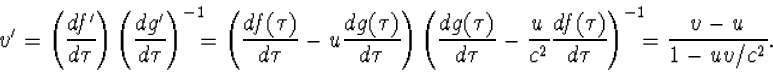$\begin{displaymath}v'=\left(\frac{df'}{d\tau}\right)\left(\frac{dg'}{d\tau}\righ... ...\frac{df(\tau)}{d\tau}\right)^{-1} \!\!\!=\frac{v-u}{1-uv/c^2}.\end{displaymath}$

(4.32)

-

Op pag. 26, in verg. (4.41), is bij de transformatie van de tijd een deelstreep weggevallen, er had moeten staan:

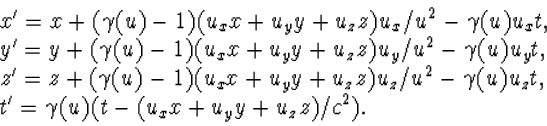$\begin{displaymath}\begin{array}{l} x'=x+(\gamma(u)-1)(u_xx+u_yy+u_z z)u_x/u^2-\... ...a(u)u_zt,\\ t'=\gamma(u)(t-(u_xx+u_yy+u_z z)/c^2). \end{array}\end{displaymath}$

(4.41)

-

Op pag. 27, net boven verg. (4.42), moet u" worden vervangen door u.

-

Op pag. 29, moet in verg. (4.57) de tweede regel beginnen met y'=en niet met x'=. De correcte uitdrukking voor de draaiing is dus:

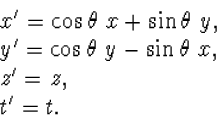$\begin{displaymath}\begin{array}{l} x'=\cos\theta~x+\sin\theta~y,\\ y'=\cos\theta~y-\sin\theta~x,\\ z'=z,\\ t'=t. \end{array}\end{displaymath}$

(4.57)

-

Op pag. 29, is verg. (4.60) uiteraard de uitdrukking voor u₄ en niet voor u₂. Dus er had moeten staan:

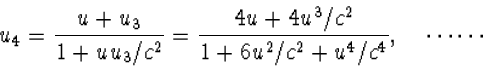$\begin{displaymath}u_4=\frac{u+u_3}{1+uu_3/c^2}=\frac{4u+4u^3/c^2}{1+6u^2/c^2+u^4/c^4},\quad \cdots\cdots\end{displaymath}$

(4.60)

-

Op pag. 29, is in verg. (4.61) de verkeerde uitdrukking voor de $\tanh$ gegeven. Er had moeten staan

$\begin{displaymath}u_n=c\tanh\varphi_n=c(e^{\varphi_n}-e^{-\varphi_n})/(e^{\varphi_n}+ e^{-\varphi_n}).\end{displaymath}$

(4.61)

-

Bovenaan op pag. 30, in verg. (4.63), moet u vervangen worden door -u. De correcte uitdrukking voor u_n luidt:

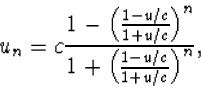$\begin{displaymath}u_n=c\frac{1-\left(\frac{1-u/c}{1+u/c}\right)^n}{1+\left(\frac{1-u/c}{1 +u/c}\right)^n},\end{displaymath}$

(4.63)

-

Op pag. 31, 2e en 3e regel boven verg. (4.64), had moeten staan $\Delta t'=t(1-(v/c)\cos\theta)$ (i.p.v. $\Delta t'=t(1+(v/c)\cos\theta)$ ).

-

Op pag. 45, in verg. (6.24) kan het tot verwarring leiden dat u is vervangen door -u, om de omkeer van de snelheidsrichting aan te geven. Het is beter het als volgt te formuleren:

Volgens de relativiteitstheorie wordt licht met frequentie $\nu$ , dat wordt uitgezonden door een lichtbron die zich met een snelheid u>0 van ons af beweegt, door ons waargenomen als licht met de verlaagde frequentie

$\begin{displaymath}\nu'=\nu\sqrt{\frac{c-u}{c+u}}.\end{displaymath}$ (6.23)

Als de lichtbron met een snelheid v=-u>0 naar ons toe beweegt zien we de verhoogde frequentie

$\begin{displaymath}\nu'=\nu\sqrt{\frac{c+v}{c-v}}.\vspace{-5mm}\end{displaymath}$ (6.24)

-

Onderaan pag. 57, in verg. (8.7), moet de eigentijd $\tau$ vervangen worden door de gewone tijd t. De correcte uitdrukking voor $p_\mu$ luidt:

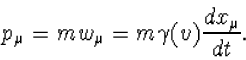$\begin{displaymath}p_\mu=mw_\mu=m\gamma(v)\frac{dx_\mu}{dt}.\end{displaymath}$

(8.7)

-

Midden op pag. 65, 3e regel boven verg. (8.31), moet voor $d(xa/c-c\gamma(v))/d\tau$ uiteraard de gelijkheid $d(xa/c-c\gamma(v))/d\tau=0$ worden gelezen.

-

In verg. (8.31) op pag. 65 zit een rekenfout. Beide gevallen van een constante versnelling, het ruimteschip en het geladen deeltje in een electrisch veld, geven hetzelfde resultaat. De tekst tussen verg. (8.31) en (8.35) moet vervangen worden door:

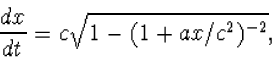$\begin{displaymath}\frac{dx}{dt}=c\sqrt{1-(1+ax/c^2)^{-2}},\end{displaymath}$

(8.31)

waarmee we x(t) bepalen (ga dit na):

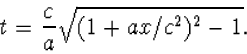$\begin{displaymath}t=\frac{c}{a}\sqrt{(1+ax/c^2)^2-1}. \end{displaymath}$

(8.32)

Voor t klein, geeft dit het niet-relativistische resultaat, $x={\scriptstyle{{1\over 2}}}at^2$ . Uit verg. (8.31) zien we eenvoudig dat de snelheid, v=dx/dt, begrensd is door de lichtsnelheid, die voor $x\rightarrow\infty$ van onderen wordt benaderd. We kunnen constante versnelling ( $d\vec p/dt=\vec F$ , $d\vec F/dt=0$ ) ook bekijken vanuit een intertiaalstelsel, zoals voor de hand ligt bij een geladen deeltje in een electrisch veld, waarover later meer. We kiezen wederom de kracht in de x-richting en definiëren a=F/m. Er geldt dw₁/dt=a, zodat $v\gamma(v)=at$ . We bepalen hieruit weer de snelheid v=dx/dt,

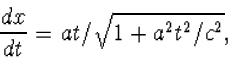$\begin{displaymath}\frac{dx}{dt}=at/\sqrt{1+a^2t^2/c^2},\end{displaymath}$

(8.33)

zodat

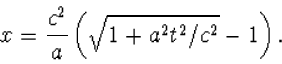$\begin{displaymath}x=\frac{c^2}{a}\left(\sqrt{1+a^2t^2/c^2}-1\right).\end{displaymath}$

(8.34)

Wederom gaat men eenvoudig na dat voor t klein, het niet-relativistische resultaat (de parabool $x={\scriptstyle{{1\over 2}}}at^2$ ) volgt en dat de snelheid begrensd is door de lichtsnelheid. In beide gevallen geldt

[1+ax(t)/c²]²-[at/c]²=1.

(8.35)

-

Op pag. 67, net boven verg. (8.41), heeft de uitdrukking voor v² het verkeerde teken, er had moeten staan: $\vec v\cdot\vec v=c^2(1-(mc^2/E)^2)$ .

-

Correcties bij de aan de syllabus toegevoegde extra opgaven: Verwijzingen naar (de aanvulling op) het dictaat moeten naar de syllabus zijn, waardoor twee maal naar een verkeerde pagina wordt verwezen (onderaan opgave 1 en 3). Echter de verwijzingen naar vergelijkingen en opgaven blijven geldig.