8.2 Electromagnetische velden

Het formuleren van een geunificeerde beschrijving van electrische en magnetische verschijnselen is één van de grote prestaties van de negentiende eeuwse natuurkunde geweest. Deze beschrijving heeft zijn uiteindelijke vorm gekregen in de theorie van Maxwell, waarin als basisgrootheden de van ruimte en tijd afhankelijke 3-dimensionale vectorgrootheden voor electrische ($\vec E(\vec x,t)$) en magnetische velden ($\vec B(\vec x,t)$) optreden, die door middel van een stelsel differentiaal vergelijkingen met elkaar zijn verbonden Hiermee kan een breed scala van fysische effecten worden begrepen. In het bijzonder is gebleken dat licht een electromagnetisch golfverschijnsel is.

Eén van de consequenties van de theorie van Maxwell is dat de voortplantingssnelheid van lichtgolven in vacuum in ieder inertiaalsysteem dezelfde waarde heeft. Zoals we gezien hebben, heeft dit feit in het begin van de 20e eeuw geleid tot de speciale relativiteitstheorie van Einstein. De Maxwell vergelijkingen die het gedrag van het electromagnetische veld beschrijven zijn al relativistisch invariant. Dit is echter niet direct duidelijk in de formulering van de theorie zoals we haar meestal leren, en zoals ze in feite oorspronkelijk door Maxwell werd opgesteld.

Aanpassing van de Maxwell theorie aan de speciale relativiteitstheorie betekent niet dat ze veranderd moet worden, maar dat ze in een 4-dimensionale vorm wordt gebracht, die de Lorentz invariantie onmiddelijk zichtbaar maakt. We hebben in hoofdstuk 7 opgemerkt dat er naast vectoren ook tensoren zijn. In de 4-dimensionale Minkowski ruimte is een Lorentz 4-tensor een grootheid die bestaat uit 16 getallen. Deze getallen, de componenten van de 4-tensor, moeten bij overgang naar een ander inertiaal systeem getransformeerd worden op een manier die wat ingewikkelder is dan wat we kennen van 4-vectoren, maar die toch ook weer bepaald wordt door de bij de overgang behorende Lorentz transformatie.

De kracht die een geladen deeltje met electrische lading q ondervindt in een electrisch en magnetisch veld wordt beschreven door de Lorentz kracht. In zg. Gaussische (cgs) eenheden,
\begin{displaymath} \vec F=q(\vec E+\vec v\times\vec B/c).\end{displaymath} (8.36)

(Voor SI (mks) eenheden, vervang overal in deze paragraaf Bi door cBi.)
Het uitwendig product, $\vec a\times\vec b$, van twee 3-dimensionale vectoren $\vec a$ en $\vec b$ is een 3-dimensionale vector met componenten gegeven door
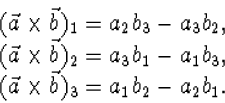\begin{displaymath} \begin{array} {l} (\vec a\times\vec b)_1=a_2b_3-a_3b_2,\\ (\... ...3b_1-a_1b_3,\\ (\vec a\times\vec b)_3=a_1b_2-a_2b_1.\end{array}\end{displaymath} (8.37)

Het is opmerkelijk dat in ieder stelsel $\vec F$ gegeven wordt door verg. (8.36). Dit betekent dat het electromagnetische veld zich op een héél speciale manier onder Lorentz transformaties gedraagt. In principe kunnen we dat afleiden uit de transfromatie van de kracht. Pas later in de studie kan volledig recht gedaan worden aan de formulering van het electromagnetische veld, we zullen hier volstaan met een korte bespreking.

De centrale grootheid in de Minkowski formulering van de Maxwell theorie is de z.g. electromagnetische veldtensor. Deze wordt gewoonlijk aangeduid als $F_{\mu\nu}$ . De indices $\mu$ en $\nu$ doorlopen ieder apart de gebruikelijke waarden 0, 1, 2 en 3. Deze veldtensor is antisymmetrisch in $\mu$ en $\nu$, en heeft daarom maar zes onafhankelijke componenten. Dit zijn precies de drie componenten van $\vec E(\vec x,t)$ plus de drie componenten van $\vec B(\vec x,t)$.
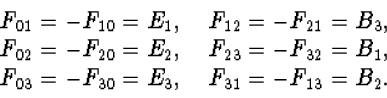\begin{displaymath} \begin{array} {l} F_{01}=-F_{10}=E_1,\quad F_{12}=-F_{21}=B_... ...=B_1,\\ F_{03}=-F_{30}=E_1,\quad F_{31}=-F_{13}=B_2.\end{array}\end{displaymath} (8.38)

Op deze manier vormen twee 3-dimensionale grootheden één 4-dimensionale grootheid. Het transformatiegedrag van deze ene grootheid onder Lorentz transformaties is aanzienlijk eenvoudiger dan dat van de twee afzonderlijke 3-dimensionale grootheden.
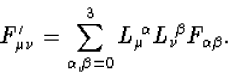\begin{displaymath} F^\prime_{\mu\nu}=\sum_{\alpha,\beta=0}^3 L_\mu{\!}^\alpha L_\nu{\!}^\beta F_{\alpha\beta}.\end{displaymath} (8.39)

Bovendien zien de Maxwell vergelijkingen er in termen van deze tensor veel eenvoudiger uit ($\sum_{\mu=0}^3\partial F_{\mu\nu}/\partial x_\mu=0$). We besluiten door op te merken dat de bewegingsvergelijking t.g.v. de Lorent kracht eenvoudig geschreven kan worden als
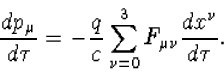\begin{displaymath} \frac{dp_\mu}{d\tau}=\frac{q}{c}\sum_{\nu=0}^3F_{\mu\nu}\frac{dx^\nu}{d\tau}.\end{displaymath} (8.40)

(Probeer zelf na te gaan dat dit inderdaad het juiste resultaat geeft.)

Tenslotte bespreken we nog kort het geval van de beweging van een geladen deeltje in een constant magnetisch veld. Wellicht weet U nog van de middelbare school dat volgens de Newtonse mechanica het geladen deeltje een cirkel- of spiraalbeweging uitvoert met een hoekfrequentie gegeven door $\omega=qB/(mc)$, de zg. Larmor frequentie. We laten eerst zien dat de grootte van de snelheid constant is. Daartoe is het voldoende aan te tonen dat E constant is (immers $\vec v\cdot\vec v=c^2(1-(mc^2/E)^2)$). Met verg. (8.28) volgt
\begin{displaymath} dE/dt=\vec v\cdot\vec F=\vec v\cdot q(\vec v\times\vec B)/c=0.\end{displaymath} (8.41)

Immers de Lorentz kracht in een magnetisch veld staat loodrecht op de snelheid (denk aan de kurketrekkerregel), zoals ook eenvoudig uit een expliciete berekening volgt. (Ga na!) Dit betekent dat we de bewegingsvergelijking kunnen schrijven als
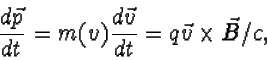\begin{displaymath} \frac{d\vec p}{dt}=m(v)\frac{d\vec v}{dt}=q\vec v\times\vec B/c,\end{displaymath} (8.42)

hetgeen precies de niet-relativistische bewegingsvergelijking is, met de massa m vervangen door m(v), hier te beschouwen als een constante. Voor de cirkelfrequentie vinden we daarom
\begin{displaymath} \omega=qB/(m(v)c)=qB/(m\gamma(v)c),\end{displaymath} (8.43)

hetgeen de relativistische Larmor frequentie is.

Opgave 23:

Kies het magneet veld langs de z-as en laat zien dat vz(t)=0, als vz(0)=0 (m.a.w. dat het deeltje in één vlak loodrecht op het magnetisch veld beweegt). Laat ook zien dat de baan van het deeltje een cirkel volgt. Bewijs de formule voor de cirkelfrequentie, verg. (8.43), en bepaal de straal van deze cirkel. Wat is de baan van het deeltje als $v_z(0) \neq 0$?

We vatten nog even de resultaten aangaande de relativistische kracht samen:

Uit de eis dat de wet van Newton in het ruststelsel geldig is volgt $d\underline{p}/d\tau=\underline{K},$ waarbij $K_0=\vec v\cdot\vec K/c$ en $\vec K=\gamma(v)\vec F$, zodat $d\vec p/dt=\vec F$.
Voor een geladen deeltje met een electrische lading q in een electromagnetisch veld wordt de Lorentz kracht in ieder stelsel gegeven door $\vec F=q(\vec E+\vec v\times\vec B/c)$.





EINDE

  • Naar inhoudsopave