- 3.
- a.
- Uit behoud van impuls volgt dat beide fotonen in het ruststelsel,
waar voor het verval de impuls nul was, na het verval in precies tegengestelde
richting van elkaar moeten bewegen. De absolute waarde p van de impuls is
dus voor beide fotonen gelijk. Beide fotonen hebben dus ook dezelfde energie
E (=pc). Uit energiebehoud volgt dan dat E=67,5 MeV. De golflengte volgt
uit
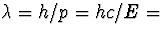
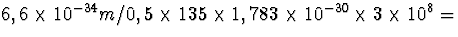
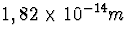 . Dit is harde gammastraling.
(1,5 punt)
. Dit is harde gammastraling.
(1,5 punt)
- b.
- i.
- We gebruiken dat
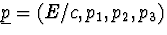 een 4-vector is. We kiezen de bewegingsrichting van het pion langs
de x-richting, zodat p1=p3=0 en
een 4-vector is. We kiezen de bewegingsrichting van het pion langs
de x-richting, zodat p1=p3=0 en 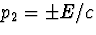 . De Lorentz transformatie
voor de p0 coefficient geeft dan
. De Lorentz transformatie
voor de p0 coefficient geeft dan 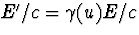 . Met
. Met 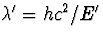 volgt dus
volgt dus 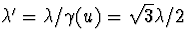 .
U kunt uiteraard ook de formule van het Doppler-effect gebruiken - die hebben
we hier in feite even afgeleid. Een andere nog kortere methode is op te merken
dat voor het verval het muon een totale energie gelijk aan
.
U kunt uiteraard ook de formule van het Doppler-effect gebruiken - die hebben
we hier in feite even afgeleid. Een andere nog kortere methode is op te merken
dat voor het verval het muon een totale energie gelijk aan 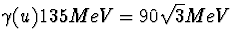 heeft. Beide fotonen houden uiteraard gelijke energie zodat
heeft. Beide fotonen houden uiteraard gelijke energie zodat
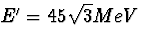 en hieruit volgt de eerder bepaalde waarde voor
en hieruit volgt de eerder bepaalde waarde voor 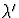 .(0,5 punt)
.(0,5 punt)
- ii.
- Onder de Lorentz transformatie geldt ook dat
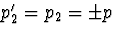 . Verder geldt dat
. Verder geldt dat 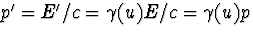 , zodat de hoek
, zodat de hoek
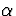 die de twee fotonen met de bewegingsrichting van het pion maken bepaald
is door
die de twee fotonen met de bewegingsrichting van het pion maken bepaald
is door 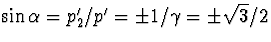 . Dus
. Dus 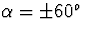 . (0,5 punt)
. (0,5 punt)
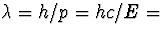
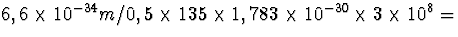
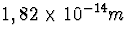 . Dit is harde gammastraling.
(1,5 punt)
. Dit is harde gammastraling.
(1,5 punt)
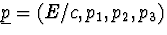 een 4-vector is. We kiezen de bewegingsrichting van het pion langs
de x-richting, zodat p1=p3=0 en
een 4-vector is. We kiezen de bewegingsrichting van het pion langs
de x-richting, zodat p1=p3=0 en 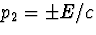 . De Lorentz transformatie
voor de p0 coefficient geeft dan
. De Lorentz transformatie
voor de p0 coefficient geeft dan 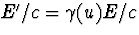 . Met
. Met 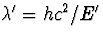 volgt dus
volgt dus 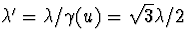 .
U kunt uiteraard ook de formule van het Doppler-effect gebruiken - die hebben
we hier in feite even afgeleid. Een andere nog kortere methode is op te merken
dat voor het verval het muon een totale energie gelijk aan
.
U kunt uiteraard ook de formule van het Doppler-effect gebruiken - die hebben
we hier in feite even afgeleid. Een andere nog kortere methode is op te merken
dat voor het verval het muon een totale energie gelijk aan 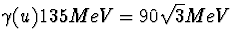 heeft. Beide fotonen houden uiteraard gelijke energie zodat
heeft. Beide fotonen houden uiteraard gelijke energie zodat
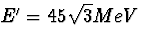 en hieruit volgt de eerder bepaalde waarde voor
en hieruit volgt de eerder bepaalde waarde voor 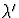 .(0,5 punt)
.(0,5 punt)
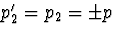 . Verder geldt dat
. Verder geldt dat 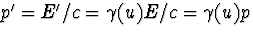 , zodat de hoek
, zodat de hoek
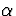 die de twee fotonen met de bewegingsrichting van het pion maken bepaald
is door
die de twee fotonen met de bewegingsrichting van het pion maken bepaald
is door 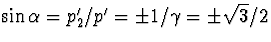 . Dus
. Dus 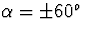 . (0,5 punt)
. (0,5 punt)