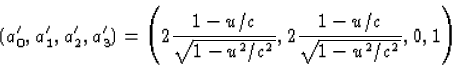- 4.
- a.
- a0=a1=2, a2=0, a3=1,
 ,
,
 is ruimteachtig. Aangezien
is ruimteachtig. Aangezien 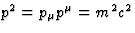 voor een
bewegend deeltje met massa m altijd positief is, kan
voor een
bewegend deeltje met massa m altijd positief is, kan 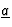 nooit
een energie-impulsviervector zijn.
nooit
een energie-impulsviervector zijn.
- b.
- Onder deze Lorentz transformatie transformeert (a0,a1,a2,a3) in
| 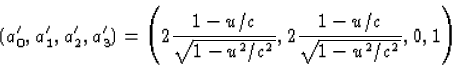 |
(18) |
We vinden dan voor de lengte: a'2=4(1-u/c)2/(1-u2/c2)-(4(1-u/c)2/(1-u2/
c2)+0+1)=-1<0. Wederom ruimteachtig. We zien ook a'2=a2. Dit is
natuurlijk altijd zo voor Lorentz transformaties; deze laten lengtes van viervectoren
invariant, en dus ook of een viervector tijd-, licht- of ruimteachtig is.
 ,
,
 is ruimteachtig. Aangezien
is ruimteachtig. Aangezien 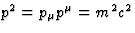 voor een
bewegend deeltje met massa m altijd positief is, kan
voor een
bewegend deeltje met massa m altijd positief is, kan 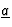 nooit
een energie-impulsviervector zijn.
nooit
een energie-impulsviervector zijn.