- 2.
-
- a.
- Gebruik hiervoor formule (4.41) uit de syllabus. Dit geeft
|  |
(8) |
- b.
- De bewegende staaf heeft in S een lengte
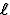 , en is daar t.g.v de
Lorentz-FitzGerald contractie een factor
, en is daar t.g.v de
Lorentz-FitzGerald contractie een factor 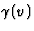 korter dan in het eigen
ruststelsel. Daar bedraagt de lengte derhalve
korter dan in het eigen
ruststelsel. Daar bedraagt de lengte derhalve 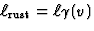 .In S' heeft de staaf met rustlengte
.In S' heeft de staaf met rustlengte  en snelheid v' een
lengte
en snelheid v' een
lengte 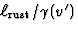 (wederom Lorentz-FitzGerald), ofwel
(wederom Lorentz-FitzGerald), ofwel
|  |
(9) |
- c.
- We lossen eerst op
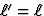 . Dit geeft
. Dit geeft 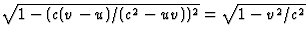 . Kwadrateren en oplossen geeft
. Kwadrateren en oplossen geeft 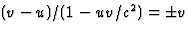 .
We behandelen de twee gevallen (
.
We behandelen de twee gevallen (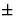 ) apart
) apart
|  |
(10) |
We vinden de volgende interpretaties. Oplossing 1 (u=0): De stelsels S en
S' vallen samen, zodat 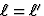 . Oplossing 2 (u=2v/(1+v2/c2)): In
stelsel S' heeft de staaf nu een snelheid -v (relativistische optelling van
snelheden!), en dus dezelfde Lorentz-FitzGerald contractie als in S, m.a.w.
. Oplossing 2 (u=2v/(1+v2/c2)): In
stelsel S' heeft de staaf nu een snelheid -v (relativistische optelling van
snelheden!), en dus dezelfde Lorentz-FitzGerald contractie als in S, m.a.w.
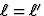 . Zorgvuldige analyse van
. Zorgvuldige analyse van
|  |
(11) |
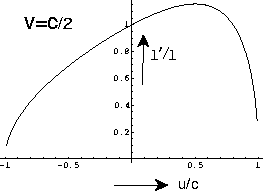
leert dat 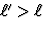 wanneer 0<u<2v/(1+v2/c2). In dit regime gaat de staaf
langzamer in S' dan in S en ondergaat deze derhalve een kleinere contractie.
Tenslotte
wanneer 0<u<2v/(1+v2/c2). In dit regime gaat de staaf
langzamer in S' dan in S en ondergaat deze derhalve een kleinere contractie.
Tenslotte 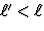 als -c<u<0 of 2v/(1+v2/c2)<u<c. Nu gaat de staaf in
S' sneller dan in S (naar rechts, resp. links) en wordt dus sterker
ingekrompen. Voor de minima en maxima: deze worden - afgezien van de randminima
in
als -c<u<0 of 2v/(1+v2/c2)<u<c. Nu gaat de staaf in
S' sneller dan in S (naar rechts, resp. links) en wordt dus sterker
ingekrompen. Voor de minima en maxima: deze worden - afgezien van de randminima
in 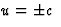 (daar is
(daar is 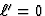 , de ultieme Lorentz-FitzGerald contractie) - gegeven door de
oplossingen van
, de ultieme Lorentz-FitzGerald contractie) - gegeven door de
oplossingen van 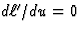 . Zo krijgt men
. Zo krijgt men
|  |
(12) |
Dit is een maximum,
|  |
(13) |
In deze situatie beweegt S' met de staaf mee, ofwel: S' is het eigen
ruststelsel van de staaf. Hier heeft de staaf geen lengte-contractie ondergaan
en is de lengte maximaal, de eigenlengte.

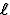 , en is daar t.g.v de
Lorentz-FitzGerald contractie een factor
, en is daar t.g.v de
Lorentz-FitzGerald contractie een factor 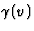 korter dan in het eigen
ruststelsel. Daar bedraagt de lengte derhalve
korter dan in het eigen
ruststelsel. Daar bedraagt de lengte derhalve 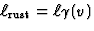 .In S' heeft de staaf met rustlengte
.In S' heeft de staaf met rustlengte  en snelheid v' een
lengte
en snelheid v' een
lengte 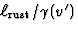 (wederom Lorentz-FitzGerald), ofwel
(wederom Lorentz-FitzGerald), ofwel

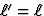 . Dit geeft
. Dit geeft 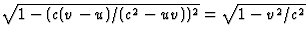 . Kwadrateren en oplossen geeft
. Kwadrateren en oplossen geeft 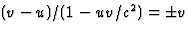 .
We behandelen de twee gevallen (
.
We behandelen de twee gevallen (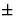 ) apart
) apart


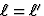 . Oplossing 2 (u=2v/(1+v2/c2)): In
stelsel S' heeft de staaf nu een snelheid -v (relativistische optelling van
snelheden!), en dus dezelfde Lorentz-FitzGerald contractie als in S, m.a.w.
. Oplossing 2 (u=2v/(1+v2/c2)): In
stelsel S' heeft de staaf nu een snelheid -v (relativistische optelling van
snelheden!), en dus dezelfde Lorentz-FitzGerald contractie als in S, m.a.w.
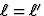 . Zorgvuldige analyse van
. Zorgvuldige analyse van

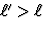 wanneer 0<u<2v/(1+v2/c2). In dit regime gaat de staaf
langzamer in S' dan in S en ondergaat deze derhalve een kleinere contractie.
Tenslotte
wanneer 0<u<2v/(1+v2/c2). In dit regime gaat de staaf
langzamer in S' dan in S en ondergaat deze derhalve een kleinere contractie.
Tenslotte 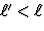 als -c<u<0 of 2v/(1+v2/c2)<u<c. Nu gaat de staaf in
S' sneller dan in S (naar rechts, resp. links) en wordt dus sterker
ingekrompen. Voor de minima en maxima: deze worden - afgezien van de randminima
in
als -c<u<0 of 2v/(1+v2/c2)<u<c. Nu gaat de staaf in
S' sneller dan in S (naar rechts, resp. links) en wordt dus sterker
ingekrompen. Voor de minima en maxima: deze worden - afgezien van de randminima
in 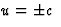 (daar is
(daar is 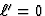 , de ultieme Lorentz-FitzGerald contractie) - gegeven door de
oplossingen van
, de ultieme Lorentz-FitzGerald contractie) - gegeven door de
oplossingen van 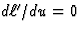 . Zo krijgt men
. Zo krijgt men

