- 10.
- Het deeltje heeft een snelheid v=0,6c in het laboratoriumstelsel S, het
electron een snelheid u'=0,75 c, in het stelsel S' van het deeltje.
- a.
- We gebruiken de relativistische optelling voor snelheden
 .
. - b.
- Om de snelheid (dx/dt,dy/dt) van het deeltje te vinden gebruiken we de Lorentz transformaties
en de kettingregel, zie de formules (4.24-36) van de syllabus. Er geldt
 . Voor de beweging van het electron
in S' geldt x'=0,y'=u't', zodat
. Voor de beweging van het electron
in S' geldt x'=0,y'=u't', zodat 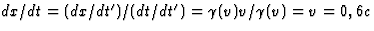 en
en 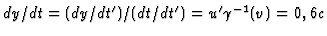 . Hieruit volgt
. Hieruit volgt
 , onder 45o met de
oorspronkelijke bewegingsrichting.
, onder 45o met de
oorspronkelijke bewegingsrichting.
- c.
- We berekenen eerst de hoek waaronder het deeltje wordt geëmitteerd.
We stellen voor de positie van het electron
 .
We eisen dx/dt=0, en vinden zo
.
We eisen dx/dt=0, en vinden zo 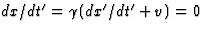 , door weer van
de Lorentz transformatie en kettingregel gebruik te maken. Hieruit volgt
, door weer van
de Lorentz transformatie en kettingregel gebruik te maken. Hieruit volgt 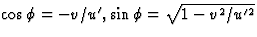 . In S' wordt het deeltje dus deels naar achteren
geschoten. Voorts
. In S' wordt het deeltje dus deels naar achteren
geschoten. Voorts
 .
En dus vtot=dy/dt=0,5625 c.
.
En dus vtot=dy/dt=0,5625 c.
 .
. . Voor de beweging van het electron
in S' geldt x'=0,y'=u't', zodat
. Voor de beweging van het electron
in S' geldt x'=0,y'=u't', zodat 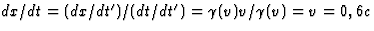 en
en 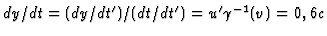 . Hieruit volgt
. Hieruit volgt
 , onder 45o met de
oorspronkelijke bewegingsrichting.
, onder 45o met de
oorspronkelijke bewegingsrichting.
 .
We eisen dx/dt=0, en vinden zo
.
We eisen dx/dt=0, en vinden zo 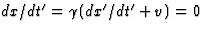 , door weer van
de Lorentz transformatie en kettingregel gebruik te maken. Hieruit volgt
, door weer van
de Lorentz transformatie en kettingregel gebruik te maken. Hieruit volgt 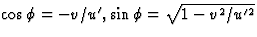 . In S' wordt het deeltje dus deels naar achteren
geschoten. Voorts
. In S' wordt het deeltje dus deels naar achteren
geschoten. Voorts
 .
En dus vtot=dy/dt=0,5625 c.
.
En dus vtot=dy/dt=0,5625 c.