Antwoord 9: Wat hier interessant is, is dat er een menging van de
versnellingscomponenten uit verschillende richtingen kan optreden. De afleiding
is vrijwel identiek aan die van de twee vorige opgaven. We gaan nu uit van
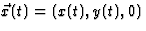 , zodanig dat in
, zodanig dat in 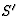 , dat t.o.v. van S
beweegt met een snelheid u langs de x-as,
, dat t.o.v. van S
beweegt met een snelheid u langs de x-as, 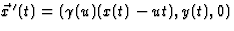 en
en 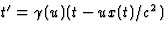 . Voor de transformatie
van de snelheid volgt hieruit dat
. Voor de transformatie
van de snelheid volgt hieruit dat ![$\vec v{\,}^\prime(t)=(d\vec x{\,}^\prime(t)
/dt)/(dt^\prime(t)/dt)=(\gamma(u)(v_x(t)-u),v_y(t),0)/[\gamma(u)(1-uv_x(t)/
c^2)]$](img91.gif) . Tenslotte volgt hieruit weer de transformatie voor de versnelling door
. Tenslotte volgt hieruit weer de transformatie voor de versnelling door
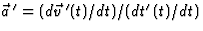 . De berekening
voor
. De berekening
voor 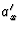 is identiek aan die van opgave 6,
is identiek aan die van opgave 6,
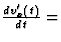
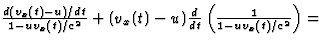


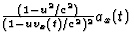 ,
,
zodat met ![$a_x^\prime=[dv^\prime_x(t)/dt]/[\gamma(u)(1-uv_x(t)/c^2)]$](img99.gif) het
gevraagde resultaat volgt. Bij de berekening van
het
gevraagde resultaat volgt. Bij de berekening van 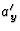 komt zowel ax
als ay voor, omdat
komt zowel ax
als ay voor, omdat 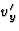 afhangt van zowel vx(t) als van vy(t).
afhangt van zowel vx(t) als van vy(t).


Met ![$a_y^\prime=[dv^\prime_y(t)/dt]/[
\gamma(u)(1-uv_x(t)/c^2)]$](img104.gif) volgt weer het gevraagde resultaat. Dat hieruit
de resultaten uit opgave 7 en 8 zijn te herleiden is evident.
volgt weer het gevraagde resultaat. Dat hieruit
de resultaten uit opgave 7 en 8 zijn te herleiden is evident.
![]()
![]()
![]()
![]()
![]() ,
,![]() het
gevraagde resultaat volgt. Bij de berekening van
het
gevraagde resultaat volgt. Bij de berekening van ![]() komt zowel ax
als ay voor, omdat
komt zowel ax
als ay voor, omdat ![]() afhangt van zowel vx(t) als van vy(t).
afhangt van zowel vx(t) als van vy(t).
![]()
![]()
![]() volgt weer het gevraagde resultaat. Dat hieruit
de resultaten uit opgave 7 en 8 zijn te herleiden is evident.
volgt weer het gevraagde resultaat. Dat hieruit
de resultaten uit opgave 7 en 8 zijn te herleiden is evident.