Antwoord 8: In dit geval vindt er in het stelsel S een versnelde
beweging in de y-richting plaats, terwijl 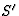 zoals gewoonlijk t.o.v.
van S beweegt met een snelheid u langs de x-as. Met
zoals gewoonlijk t.o.v.
van S beweegt met een snelheid u langs de x-as. Met 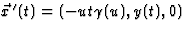 en
en 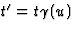 , vinden we dus eenvoudig
, vinden we dus eenvoudig
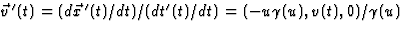 . (Merk op dat dit dus het resultaat voor het
optellen niet evenwijdige snelheden geeft.) Hieruit volgt de versnelling
door
. (Merk op dat dit dus het resultaat voor het
optellen niet evenwijdige snelheden geeft.) Hieruit volgt de versnelling
door 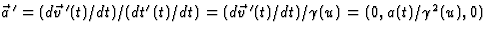 .
.