Antwoord 7: Gebruikmakende van 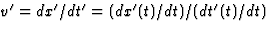 , met
, met 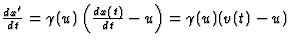 en
en 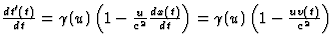 , volgt dus
, volgt dus 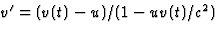 ,
als gegeven in verg. (4.30). Dit is ook de formule voor het optellen van
snelheden (let op het teken van u). Omdat we nu
,
als gegeven in verg. (4.30). Dit is ook de formule voor het optellen van
snelheden (let op het teken van u). Omdat we nu 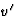 als een functie
van t hebben, kunnen we hieruit de versnelling in het stelsel
als een functie
van t hebben, kunnen we hieruit de versnelling in het stelsel 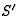 afleiden door te gebruiken dat
afleiden door te gebruiken dat 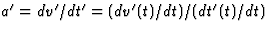 . Al eerder werd
. Al eerder werd 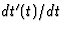 bepaald, terwijl
bepaald, terwijl
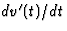 berekend wordt met behulp van de expliciete uitdrukking voor
berekend wordt met behulp van de expliciete uitdrukking voor
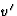 als een functie van t,
als een functie van t,
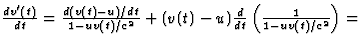
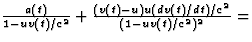
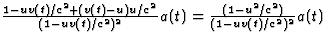 ,
,
samen met 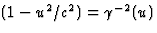 vinden we nu eenvoudig verg. (4.36),
vinden we nu eenvoudig verg. (4.36),
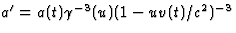 .
.
![]()
![]()
![]() ,
,![]() vinden we nu eenvoudig verg. (4.36),
vinden we nu eenvoudig verg. (4.36),
![]() .
.