Antwoord 4: In deze opgave moeten we zorgvuldig snelheden bij elkaar
optellen. Gegeven is de richting en grootte van de etherwind (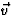 ) en de
grootte (c) van de lichtsnelheid t.o.v. de ether. We moeten nu de richting
van deze lichtsnelheid in beide armen van de interferometer, voor zowel de
heen- als de terugreis van het licht, zodanig kiezen dat de som van
) en de
grootte (c) van de lichtsnelheid t.o.v. de ether. We moeten nu de richting
van deze lichtsnelheid in beide armen van de interferometer, voor zowel de
heen- als de terugreis van het licht, zodanig kiezen dat de som van 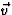 en
en 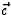 langs een van de twee armen wijst. Hieruit moet dan de grootte van
de resulterende snelheid volgen, waarmee het licht zich langs de armen beweegt.
Voor de arm met lengte dk, schrijven we ckh voor de snelheid bij de
heenreis en ckt voor de snelheid bij de terugreis (met uiteraard k=1 of
2). Er zijn verschillende manieren om c1,2h,t te brekenen. We laten
ons daarbij leiden door de fysische vraagstelling. De situatie is in de figuur
weergegeven voor de berekening van c1h.
langs een van de twee armen wijst. Hieruit moet dan de grootte van
de resulterende snelheid volgen, waarmee het licht zich langs de armen beweegt.
Voor de arm met lengte dk, schrijven we ckh voor de snelheid bij de
heenreis en ckt voor de snelheid bij de terugreis (met uiteraard k=1 of
2). Er zijn verschillende manieren om c1,2h,t te brekenen. We laten
ons daarbij leiden door de fysische vraagstelling. De situatie is in de figuur
weergegeven voor de berekening van c1h.
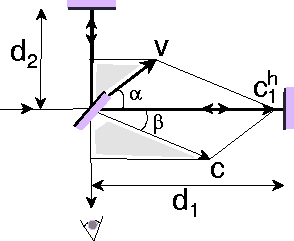
We willen dat de component van 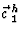 in de richting loodrecht
op de horizontale arm nul is. Met de hulphoek
in de richting loodrecht
op de horizontale arm nul is. Met de hulphoek 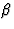 betekent dit dat
betekent dit dat
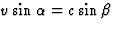 . Hieruit kunnen we
. Hieruit kunnen we 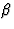 elimineren, i.h.b geldt
elimineren, i.h.b geldt
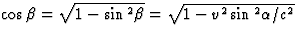 . Met
deze hulphoek
. Met
deze hulphoek 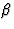 kunnen we nu ook eenvoudig c1h bepalen als de
som van de twee componenten langs de horizontale arm,
kunnen we nu ook eenvoudig c1h bepalen als de
som van de twee componenten langs de horizontale arm, 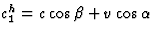 . Voor de terugreis van het licht verandert alleen dat we nu het
verschil van de twee horizontale componenten moeten nemen (de verticale
componenten moeten het zelfde blijven om de lichtstraal horizontaal te houden).
Dus geldt
. Voor de terugreis van het licht verandert alleen dat we nu het
verschil van de twee horizontale componenten moeten nemen (de verticale
componenten moeten het zelfde blijven om de lichtstraal horizontaal te houden).
Dus geldt 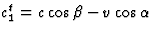 . De totale looptijd van het licht,
heen en terug, is nu dus
. De totale looptijd van het licht,
heen en terug, is nu dus 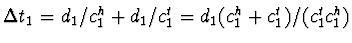 . We vinden dat
. We vinden dat 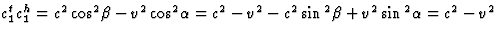 , zodanig dat
, zodanig dat 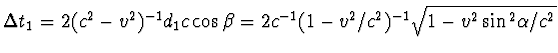 . Tenslotte hadden we aangenomen dat iedere arm van de
interferometer een contractie ondergaat, bepaald door de snelheidscomponent
van de ether langs de arm. Voor de horizontale arm betekent dit een contractie
met een factor
. Tenslotte hadden we aangenomen dat iedere arm van de
interferometer een contractie ondergaat, bepaald door de snelheidscomponent
van de ether langs de arm. Voor de horizontale arm betekent dit een contractie
met een factor 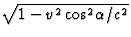 . Na deze correctie vinden we
. Na deze correctie vinden we
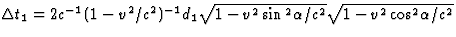 . Voor de verticale arm is
de analyse precies dezelfde indien we
. Voor de verticale arm is
de analyse precies dezelfde indien we 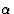 vervangen door
vervangen door 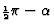 , en natuurlijk d1 door d2. Hieronder wisselen de sinus en de
cosinus van plaats, maar dit laat de uitdrukking voor
, en natuurlijk d1 door d2. Hieronder wisselen de sinus en de
cosinus van plaats, maar dit laat de uitdrukking voor 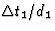 onveranderd. Het gevraagde resultaat voor
onveranderd. Het gevraagde resultaat voor 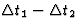 volgt nu
uit
volgt nu
uit 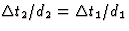 .
.

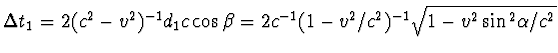 . Tenslotte hadden we aangenomen dat iedere arm van de
interferometer een contractie ondergaat, bepaald door de snelheidscomponent
van de ether langs de arm. Voor de horizontale arm betekent dit een contractie
met een factor
. Tenslotte hadden we aangenomen dat iedere arm van de
interferometer een contractie ondergaat, bepaald door de snelheidscomponent
van de ether langs de arm. Voor de horizontale arm betekent dit een contractie
met een factor