Antwoord 23: De versnelling 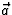 , dus de verandering van de snelheid
per tijdseenheid, is gegeven door
, dus de verandering van de snelheid
per tijdseenheid, is gegeven door 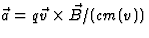 . Deze
vector staat zowel loodrecht op
. Deze
vector staat zowel loodrecht op 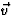 als loodrecht op
als loodrecht op 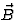 . Maar als
. Maar als
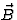 in de z-richting wijst,
in de z-richting wijst, 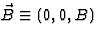 , dan staat de
versnelling dus loodrecht op deze z-richting en is dus dvz(t)/dt=0.
Indien nu vz=0 op t=0, dan geldt dit voor alle tijden. In het algemeen
als
, dan staat de
versnelling dus loodrecht op deze z-richting en is dus dvz(t)/dt=0.
Indien nu vz=0 op t=0, dan geldt dit voor alle tijden. In het algemeen
als  op t=0 dan blijft vz constant in de tijd - dat hebben we
verderop nodig. Nemen we nu vz=0, dan is de beweging in een vlak loodrecht
op de z-as, dus loodrecht op het magnetisch veld. We zagen al eerder dat
versnelling
op t=0 dan blijft vz constant in de tijd - dat hebben we
verderop nodig. Nemen we nu vz=0, dan is de beweging in een vlak loodrecht
op de z-as, dus loodrecht op het magnetisch veld. We zagen al eerder dat
versnelling 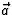 ook loodrecht op de snelheid
ook loodrecht op de snelheid 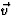 is. Omdat
is. Omdat
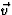 (met vz=0) zelf loodrecht op
(met vz=0) zelf loodrecht op 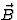 staat is de grootte
van de versnelling gelijk aan a=qvB/(cm(v)), waarbij zoals gewoonlijk
staat is de grootte
van de versnelling gelijk aan a=qvB/(cm(v)), waarbij zoals gewoonlijk
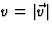 . Als U daar niet zeker van bent, gebruik dan verg. (8.37) met
. Als U daar niet zeker van bent, gebruik dan verg. (8.37) met
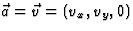 en
en 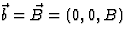 , zodat
, zodat 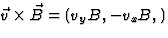 , en dus
, en dus 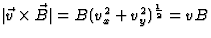 .
Omdat we eerder in de syllabus al hadden afgeleid dat de grootte van de
snelheid constant is, is dit precies de conditie voor een cirkelbeweging, die
bepaald wordt door een constante versnelling loodrecht op de constante
omloopsnelheid. Deze omloopsnelheid is gelijk aan de straal r maal de
hoeksnelheid
.
Omdat we eerder in de syllabus al hadden afgeleid dat de grootte van de
snelheid constant is, is dit precies de conditie voor een cirkelbeweging, die
bepaald wordt door een constante versnelling loodrecht op de constante
omloopsnelheid. Deze omloopsnelheid is gelijk aan de straal r maal de
hoeksnelheid 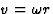 , terwijl de centrifugale versnelling is in everwicht
met de versnelling
, terwijl de centrifugale versnelling is in everwicht
met de versnelling  is. Hieruit kunnen we zowel de Larmor
frequentie als straal oplossen:
is. Hieruit kunnen we zowel de Larmor
frequentie als straal oplossen: 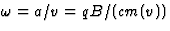 en
r=v2/a=vcm(v)/(qB). Als tenslotte
en
r=v2/a=vcm(v)/(qB). Als tenslotte 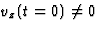 , dan ontbinden we
, dan ontbinden we
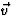 in een vector
in een vector 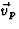 parallel aan
parallel aan 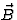 en een vector
en een vector
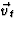 loodrecht daarop (de index t staat voor transversaal). Dus
loodrecht daarop (de index t staat voor transversaal). Dus
 en
en  . We zien echter eenvoudig
in dat het uitwendig product van twee evenwijdige vectoren altijd nul is,
zodat
. We zien echter eenvoudig
in dat het uitwendig product van twee evenwijdige vectoren altijd nul is,
zodat 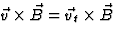 . De versnelling staat dus
nog steeds loodrecht op de z-as. De grootte van de versnelling is nu
a=qvtB/(cm(v)). De beweging kan dus ontbonden worden in een constante
beweging met snelheid vz in de z-richting en cirkelbeweging in het
x-y-vlak, met als hoekfrequentie
. De versnelling staat dus
nog steeds loodrecht op de z-as. De grootte van de versnelling is nu
a=qvtB/(cm(v)). De beweging kan dus ontbonden worden in een constante
beweging met snelheid vz in de z-richting en cirkelbeweging in het
x-y-vlak, met als hoekfrequentie  en als straal
r=vt2/a=vtcm(v)/(qB). Dit is dus een spiraalbeweging. De hoekfreqentie
hangt in het niet-relativistische geval (waar we m(v)=m stellen) niet
van de snelheid af en in het relativistische geval alleen maar van de grootte
van de totale snelheid. Dit zijn belangrijke resultaten waarmee men in
de astro- en plasmafysica uit de remstraling informatie kan verkrijgen over
de grootte van het magneetveld en de snelheden van de geladen deeltjes.
en als straal
r=vt2/a=vtcm(v)/(qB). Dit is dus een spiraalbeweging. De hoekfreqentie
hangt in het niet-relativistische geval (waar we m(v)=m stellen) niet
van de snelheid af en in het relativistische geval alleen maar van de grootte
van de totale snelheid. Dit zijn belangrijke resultaten waarmee men in
de astro- en plasmafysica uit de remstraling informatie kan verkrijgen over
de grootte van het magneetveld en de snelheden van de geladen deeltjes.