Antwoord 21: Vóór deze opgave werd ook gevraagd na te gaan
dat 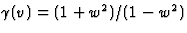 . Laten we dit eerst bewijzen:
. Laten we dit eerst bewijzen: 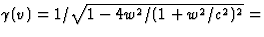
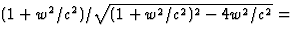
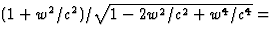 (1+w2/c2)/(1-w2/c2). De
uitdrukking voor M(w) halen we óf uit energiebehoud: (m+m(v))=M(w), samen
met m(v)=m(1+w2/c2)/(1-w2/c2), volgt dan M(w)=m[(1-w2/c2)+(1+w2/c2)]/
(1-w2/c2)=2m/(1-w2/c2), óf uit impulsbehoud,
(1+w2/c2)/(1-w2/c2). De
uitdrukking voor M(w) halen we óf uit energiebehoud: (m+m(v))=M(w), samen
met m(v)=m(1+w2/c2)/(1-w2/c2), volgt dan M(w)=m[(1-w2/c2)+(1+w2/c2)]/
(1-w2/c2)=2m/(1-w2/c2), óf uit impulsbehoud, 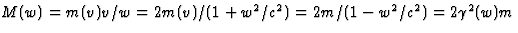 . Aangezien
. Aangezien 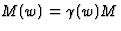 ,volgt dus voor de rustmassa
,volgt dus voor de rustmassa 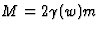 . Omdat we aannemen dat er
geen energie verloren is gegaan, moet dus de energietoename van Mc2 t.o.v.
van 2mc2 toegeschreven worden aan de bewegingsenergie van de twee
oorsponkelijke deeltjes. Niet-relativisitisch, of in laagste orde in w/c,
is deze bewegings- of kinetische energie
. Omdat we aannemen dat er
geen energie verloren is gegaan, moet dus de energietoename van Mc2 t.o.v.
van 2mc2 toegeschreven worden aan de bewegingsenergie van de twee
oorsponkelijke deeltjes. Niet-relativisitisch, of in laagste orde in w/c,
is deze bewegings- of kinetische energie 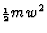 voor ieder van de twee
deeltjes. Inderdaad geldt dat
voor ieder van de twee
deeltjes. Inderdaad geldt dat 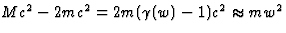 .
.