Antwoord 15: In de figuur is voor de eenvoud aangenomen dat de versnelling instantaan is. Dat maakt voor de argumenten niet echt uit; de ruimteschepen A en B volgen vanuit de aarde bezien (het stelsel S met de coordinaten x en t) dezelfde versnelling en gaan op het zelfde tijdstip t₀ over in een eenparig rechtlijnige beweging met dezelfde snelheid. Vanuit S bezien blijft de afstand tussen de twee ruimteschepen gelijk aan de lengte van de kabel op t_-1. Maar de afstand tussen de twee ruimteschepen in hun ruststelsel, 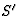, is bepalend voor de vraag of de kabel lang genoeg is. De door ons waargenomen afstand tussen de ruimteschepen ondergaat echter een Lorentz contractie, en dus is de afstand in het rustselsel (voor t>t₀) groter dan de lengte van de kabel. De conclusie is dus dat de kabel (of het ruimteschip) zal breken.

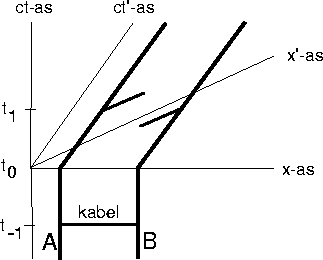
Alternatief zien we aan het verloop van de 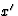-as in het ruststelsel van de twee ruimteschepen, dat A en B helemaal niet gelijktijdig versneld hebben. Verontwaardigd zal de astronaut in A zijn collega in B ervan betichten te vroeg zijn motor te hebben ontstoken, en dat hij daarmee de kabel kapot heeft getrokken (totdat hij hoort dat ook B de instructies van mission control heeft gevolgd). Uiteraard gaan we er bij deze opgave vanuit dat de kabel (ter bescherming van het ruimteschip) geen trekkracht kan verdragen, zodat B niet A op ``sleeptouw'' kan nemen.