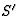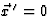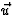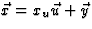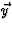Antwoord 10: Voor de oorsprong van het stelsel $S^\prime$ geldt $\vec x{\,}^\prime=0$. We ontbinden nu $\vec x$ in een component gericht langs $\vec u$ en een component daar loodrecht op, $\vec x=x_u\vec u+\vec y$. Uit het feit dat we $\vec y$ loodrecht op 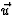$\vec u$ kiezen, 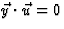$\vec y\cdot\vec u=0$, volgt dat 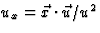$u_x=\vec x\cdot\vec u/u^2$ (ga na). We vinden dan 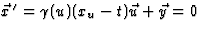$\vec x{\,}^\prime=\gamma(u) (x_u-t)\vec u+\vec y=0$, maar dat betekent dat 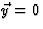$\vec y=0$ en xu=t, zodat 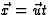$\vec x=\vec u t$. Voor een lichtstraal nemen $\vec x=\vec c t$, en we vinden $\vec x{\,}^\prime=(\vec c+\alpha\vec u)t$. Hier hebben we een compacte notatie ingevoerd om schrijfwerk te beperken, $\alpha\equiv(\gamma-1)(\vec u\cdot\vec c )/u^2-\gamma$ (ga na). 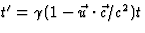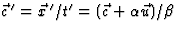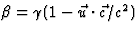Anderzijds geldt dat $t^\prime=\gamma(1-\vec u\cdot\vec c/c^2)t$, zodat $\vec c{\,}^\prime=\vec x{\,}^\prime/t^\prime=(\vec c+\alpha \vec u)/\beta$, met $\beta=\gamma(1-\vec u\cdot\vec c/c^2)$. Laten we, voordat we algemeen bewijzen dat $\vec c{\,}^\prime$ inderdaad lentge c heeft, eerst een eenvoudig speciaal geval bekijken. 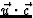Duidelijk is dat de term $\vec u\cdot \vec c$ ons het leven moeilijk maakt. 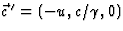Kiezen we echter $\vec u$ in de x-richting en $\vec c$ in de y-richting (in S) dan is $\vec u\cdot\vec c= 0$ en $\vec c{\,}^\prime=(-u,c/\gamma,0)$. 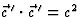We zien dat dit precies zo is dat $\vec c{\,}^\prime\cdot\vec c{\,}^\prime=c^2$ (ga na). 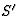Aan dit speciale voorbeeld zien we bovendien dat de hoek waaronder de lichtstraal in S wordt uitgezonden, voor een waarnemer in $S^\prime$ in het algemeen verandert (meesleep effect), zie ook opgave 18. 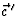Merk ook op dat we dit resultaat voor $\vec c{\,}^\prime$ evenzo met het resultaat uit opgave 8 af hadden kunnen leiden. Nu het algemene geval. 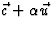We bepalen eerst de lengte van de vector $\vec c+\alpha \vec u$. Er geldt $(\vec c+\alpha \vec u)\cdot(\vec c+\alpha\vec u)=\vec c\cdot\vec c+2\alpha\vec u\cdot\vec c+\alpha^2\vec u\cdot\vec u=c^2+ 2\alpha\vec u\cdot\vec c+\alpha^2u^2$. 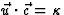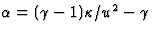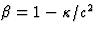We noemen nu $\vec u\cdot\vec c=\kappa$,zodat $\alpha=(\gamma-1)\kappa/u^2-\gamma$ en $\beta=1-\kappa/c^2$. We vinden dus $\vec c{\,}^\prime\cdot\vec c{\,}^\prime=(c^2+\alpha^2 u^2+2\alpha\kappa)/ \beta^2=$ $c^2(1+\{[(\gamma-1)\kappa/u^2-\gamma]u^2/c^2+2\kappa/c^2\}\alpha)/ \beta^2=$ $c^2(1+\{(\gamma+1)\kappa/c^2-\gamma u^2/c^2\}\alpha)/\beta^2=$ $c^2(1+(\gamma^2-1)\kappa^2/(u^2c^2)+\gamma^2u^2/c^2-2\gamma^2\kappa/c^2) /\beta^2$. Ga dit weer na. Tenslotte volgt nu $\vec c{\,}^\prime\cdot\vec c{\,}^\prime=c^2\gamma^2(1+\kappa^2/c^4-2\kappa/c^2)/\beta^2=c^2$. 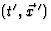Hiermee hebben we dus bewezen dat $(t^\prime,\vec x{\,}^\prime)$ inderdaad een Lorentz transformatie geeft; zie de algemene overwegingen in hoofstuk 5 van de syllabus.