Landauer formulas

Landauer's original 1957 formula [2],

$$G=\frac{2e^{2}}{h}\frac{t}{1-t},$$

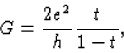
expresses the conductance of a one-dimensional system as the ratio of transmission and reflection probabilities. As explained by Imry [3], this formula gives infinity for unit transmission because it excludes the finite contact conductance contained in [30]

$$G=\frac{2e^{2}}{h}t.$$

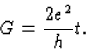
Extension to higher dimensions [31] is achieved by replacing the transmission probability t by the eigenvalue t_n of the transmission matrix product ${\bf t}{\bf t}^{\dagger}$, and summing over n.

Generalizations of the Landauer formula have been found for a variety of other transport properties, besides the conductance [32]. At zero temperature, these expressions are of the form:

$$\mbox{transport property}=A_{0}\sum_{n}a(t_{n}),$$

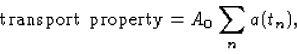
• conductance G: A₀=2e²/h, a(t)=t.
• shot-noise power P: A₀=4e³V/h, a(t)=t(1-t).
• conductance $G_{\rm NS}$ of a normal-metal - superconductor junction: A₀=4e²/h, a(t)=t²(2-t)^-2.
• supercurrent I through a Josephson junction with phase difference $\phi$: $A_{0}=e\Delta/\hbar$, $a(t)=\frac{1}{2}t\sin\phi(1-t\sin^{2}\phi/2)^{-1/2}$.

The expressions for the thermo-electric coefficients involve an integration over energies around the Fermi energy $E_{\rm F}$, weighted by the derivative f'=df/dE of the Fermi-Dirac distribution function at temperature T:

$$\mbox{transport property}=-A_{0}\int dE\,(E-E_{\rm F})^{p}f'\sum_{n}t_{n},$$

• electrical conductance G: p=0, A₀=2e²/h.
• thermo-electric coefficient L: p=1, A₀=2e/hT.
• thermal conductance K: p=2, A₀=-2/hT.

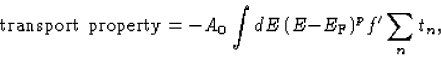
If the energy-dependence of the transmission eigenvalues is small on the scale of the thermal energy kT, one has approximately K=-L₀TG (the Wiedemann-Franz law) and $L=eL_{0}TdG/dE_{\rm F}$, with $L_{0}=\pi^{2}k^{2}/3e^{2}$ the Lorentz number.

Each Landauer formula predicts a specific quantum-size effect in a ballistic constriction, for which t_n equals 0 or 1. The effect is a step-function dependence on the width of the constriction in the case of G, $G_{\rm NS}$, $I(\phi)$, K, and an oscillatory dependence in the case of P, L.