Solid-state electron optics

The effects discussed so far refer to properties of the quantum point contact itself. A wealth of new phenomena has been discovered using a quantum point contact as a spatially coherent point source and detector, and specially formed electrodes as mirror, prism, or lens.

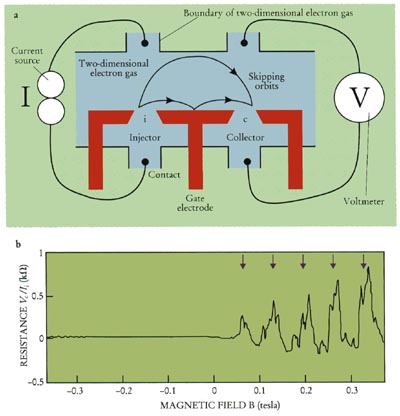
Figure 7. Magnetic focusing in a 2D electron gas at $50\,{\rm mK}$. The inset shows the experimental arrangement. Electrons injected through one point contact (i) follow skipping orbits over a distance of $3.0\,\mu{\rm m}$ to a second point contact (c). The arrows indicate the positions of the focusing peaks expected when the point contact separation is a multiple of the cyclotron diameter. The fine-structure on the peaks is due to quantum interference. (Adapted from ref. [24].)

The basic experiment [24], coherent electron focusing, is shown in figure 7. A point contact injects electrons with the Fermi momentum $p_{\rm F}$ into the 2D electron gas, in the presence of a perpendicular magnetic field B. The electrons follow a "skipping orbit" along the boundary, consisting of circular arcs of cyclotron diameter $d_{\rm c}=2p_{\rm F}/eB$. Some of the electrons are collected at a second point contact, at a separation L from the first. The voltage measured at the collector is proportional to the transmission probability between the two point contacts. V. S. Tsoi (Moscow) first used this focusing technique in a metal [25]. The magnetic field acts as a lens, bringing the divergent trajectories at the injector together at the collector. The collector is at a focal point of the lens when L is a multiple of $d_{\rm c}$, hence when B is a multiple of $2p_{\rm F}/eL$ (arrows in figure 7). For reverse magnetic fields the injected electrons are deflected away from the collector, so that no signal is generated. The observation of peaks at the expected positions demonstrates that a quantum point contact acts as a monochromatic point source of ballistic electrons, and that the reflections at the boundary of the 2D electron gas are specular. The fine-structure on the focusing peaks is due to quantum interference of trajectories between the two point contacts. Such fine-structure does not appear in metals. It demonstrates that the quantum point contact is a spatially coherent source and that the phase coherence is maintained over a distance of several microns to the collector.

Magnetic focusing has been used by several groups to obtain information on the dynamics and scattering of quasiparticles in the 2D electron gas. An intriguing application in the regime of the fractional quantum Hall effect is the focusing of composite fermions [26], which can be thought of as electrons bound to an even number of flux quanta. In the regime of the integer quantum Hall effect, the geometry of figure 7 has been used to selectively populate and detect the magnetic edge states mentioned earlier [6]. The observation of plateaus in the Hall conductance at anomalously quantized values provides support for the edge-state theory of the quantum Hall effect.

Electrostatic focusing, by means of the electric field produced by a lens-shaped electrode, provides an alternative technique to focus the beam of electrons injected by a point contact [27]. Instead of focusing the beam, one can also deflect it -- either by means of a magnetic field [28], or by means of a prism-shaped electrode [29]. The building blocks of electron optics in the solid state have by now all been realized.