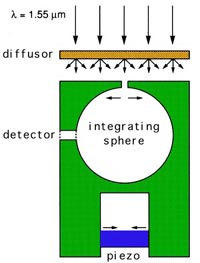
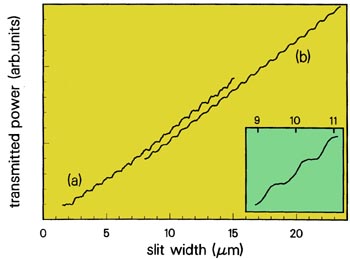
The interpretation of conduction as transmission of electrons at the Fermi level suggests an analogy with the transmission of monochromatic light [13]. The analogue of the conductance is the transmission cross-section, defined as the transmitted power divided by the incident flux. Figure 4 shows the transmission cross-section of a slit of variable width, measured by Edwin Montie and collaborators from Philips [14]. Steps of equal height occur whenever the slit width W equals half the wave length
of the light. Because
equals W for large slit widths, the step height is also equal to
. Two-dimensional isotropic illumination was achieved by passing the light through a random array of glass fibres parallel to the slit. The isotropy of the illumination mimics the reservoirs in the electronic case, and is crucial for the effect. The two-dimensionality is not essential, but was chosen because a diaphragm of variable area of the order of
is difficult to fabricate. (For a diaphragm, the steps in
are
.)
Figure 4. Equidistant steps in the optical transmission cross-section of a slit of adjustable width. A 2D isotropic illumination is obtained by shining a beam from a diode laser (
, polarization parallel to the slit) onto a diffusor consisting of a random array of parallel glass fibers. (Adapted from ref. [14].)
It is remarkable that this optical phenomenon, with its distinctly nineteenth century flavour, was not noticed prior to the discovery of its electronic counterpart. There is an interesting parallel in the history of the discovery of the two phenomena. In the electronic case, the Landauer formula was already known before the quantized conductance of a point contact was discovered. Yoseph Imry (Weizmann Institute, Israel) had made the connection with Sharvin's work on point contacts [3]. The reason that the conductance quantization came as a surprise, was that the relation
for ballistic transport was regarded as an order-of-magnitude estimate. To have quantization, the relative error in this estimate must be smaller than 1/N, which is not obvious. The equivalent of the Landauer formula for the transmission cross-section has long been familiar in optics [15], but also in this field it was not noticed that
holds with better than 1/N relative accuracy.
One can speak of the optical analogue as a quantum point contact for photons. Can the analogue be extended towards a quantum point contact for Cooper pairs? The answer is "Yes": The maximal supercurrent through a narrow and short, impurity-free constriction in a superconductor is an integer multiple of
, with
the energy gap of the bulk superconductor [16]. A superconducting quantum point contact has been realized by Hideaki Takayanagi and collaborators (NTT, Japan) [17], but the superconducting analogue of the quantized conductance remains to be observed experimentally.