 (grootte en richting) op een afstand z boven het midden tussen twee gelijke puntladingen
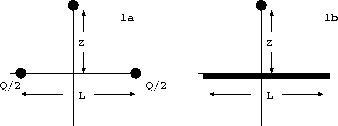
(grootte en richting) op een afstand z boven het midden tussen twee gelijke puntladingen  . De afstand tussen de ladingen is L. (Zie figuur 1a.)
. De afstand tussen de ladingen is L. (Zie figuur 1a.)(b) Bereken
 op een afstand z boven het midden van een draad van lengte L, die uniform geladen is met totale lading Q. (Zie figuur 1b.)
op een afstand z boven het midden van een draad van lengte L, die uniform geladen is met totale lading Q. (Zie figuur 1b.)(c) Wat wordt
 uit opgave b als
uit opgave b als  ?
?
Wellicht zijn de volgende integralen nuttig om te weten:
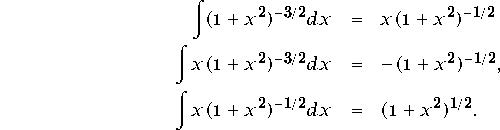
 , waarbij
, waarbij  een constante is en
een constante is en  een eenheidsvector in de z-richting. Bereken het bijbehorende magnetische veld.
een eenheidsvector in de z-richting. Bereken het bijbehorende magnetische veld.(b) Construeer een ijktransformatie van
 naar
naar  .
.(c) Hoe verandert de scalaire potentiaal
 door deze transformatie?
door deze transformatie?(d) Stel dat
 niet constant is, maar van de tijd afhangt volgens
niet constant is, maar van de tijd afhangt volgens  . Wat is dan het magnetische veld?
. Wat is dan het magnetische veld?
 en
en  . Leg uit wat de gebruikte symbolen betekenen. Geef expliciet aan waar de geretardeerde tijd voorkomt in Uw formules. Geef ook de definitie van de geretardeerde tijd.
. Leg uit wat de gebruikte symbolen betekenen. Geef expliciet aan waar de geretardeerde tijd voorkomt in Uw formules. Geef ook de definitie van de geretardeerde tijd.(b) Een puntlading beweegt met constante snelheid v naar rechts langs de x-as. Bereken de potentialen op de x-as rechts van de lading.
 beweegt ten opzichte van inertiaalstelsel S met een snelheid v in de x-richting.
beweegt ten opzichte van inertiaalstelsel S met een snelheid v in de x-richting.(a) Leid uit de Lorentztransformatie van ruimte en tijd de relatie af tussen de partiële afgeleiden
 in stelsel S en
in stelsel S en
 in stelsel
in stelsel  .
.(b) Neem als uitgangspunt dat de Maxwellvergelijking
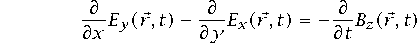
invariant is onder Lorentztransformatie. Leid hieruit af bepaalde transformatieregels voor de elektrische en magnetische velden.