Doppler-effect

6.6 Doppler-effect

Het Doppler-effect kennen we uit het dagelijkse leven. De toon van de sirene van een brandweerauto klinkt hoger als de auto naar ons toe rijdt en lager als de auto zich van ons af beweegt. We horen dat goed op het moment dat de auto ons passeert.

Het Doppler-effect is een elementair fysisch verschijnsel dat optreedt bij alle trillingsverschijnselen die zich voortplanten. Een monochromatische golf die zich in de 1-dimensionale ruimte beweegt wordt beschreven door de algemene formule

$\begin{displaymath} \varphi(x,t)=A\sin(kx-\omega t)+B\cos(kx-\omega t).\end{displaymath}$ (6.14)

We noemen k het golfgetal en $\omega$ de cirkelfrequentie. De constanten A en B geven de amplitude van de golf en de beginconditie. Voor de eenvoud veronderstellen we $\varphi(0,0)=0$ . Dan geldt B=0. We hebben dan

$\begin{displaymath} \varphi(x,t)=A\sin(kx-\omega t).\end{displaymath}$ (6.15)

We nemen deze formule eerst op een vast tijdstip. De maxima van $\varphi$ worden gegeven door $kx-\omega t=(2n+{\scriptstyle{{1\over 2}}})\pi$ . De afstand tussen twee op elkaar volgende maxima noemen we de golflengte en geven we aan met $\lambda$ . Het is duidelijk dat deze golflengte gelijk is aan $2\pi/\vert k\vert$ . Als we vervolgens formule (6.15) voor een vaste x bekijken zien we dat de tijd tussen twee op elkaar volgende maxima gelijk is aan $2\pi/\omega$ . Dit betekent dat de gewone frequentie $\nu$ gelijk is aan $\omega/(2\pi)$ . Tenslotte zien we dat een maximum zich beweegt met een snelheid $v=\omega/k$ . Voor de absolute waarde van v geldt dan $\vert v\vert=\nu\lambda$ . We noemen v de voortplantingssnelheid van de golf. Een 1-dimensionale monochromatische golf wordt dus in het algemeen bepaald door constanten A en B, en door drie parameters $\lambda$ , $\nu$ en v, waarvan er twee onafhankelijk zijn. We vatten de belangrijkste relaties nog even samen

$\begin{displaymath} \lambda=2\pi/\vert k\vert,\qquad\nu=\omega/(2\pi),\qquad v=\omega/k=\pm\nu\lambda.\end{displaymath}$ (6.16)

We veronderstellen dat de waarde die de amplitude $\varphi$ op een zeker moment op een bepaalde plaats aanneemt onafhankelijk is van het inertiaalsysteem waarin we ons bevinden. We kunnen dan met behulp van een Lorentz transformatie overgaan van het gegeven systeem S, met coördinaten x, t, naar een nieuw systeem S', met x', t'. In de nieuwe coördinaten wordt de golf beschreven door een nieuwe functie $\varphi'(x',t')=\varphi(x,t)$ . Met de formule (4.22) voor de inverse van een Lorentz transformatie schrijven we

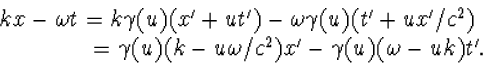$\begin{displaymath} \begin{array} {l} kx-\omega t=k\gamma(u)(x'+ut')-\omega\gamm... ...d=\gamma(u)(k-u\omega/c^2)x'-\gamma(u)(\omega-uk)t'.\end{array}\end{displaym ath}$ (6.17)

Daarmee wordt de uitdrukking voor $\varphi'$ gelijk aan

$\begin{displaymath} \varphi'(x',t')=A\sin(k'x'-\omega't'),\end{displaymath}$ (6.18)

met

$\begin{displaymath} k'=\gamma(u)(k-u\omega/c^2),\qquad\omega'=\gamma(u)(\omega-uk)t'.\end{displaymath}$ (6.19)

We hebben dus in S' een golfbeweging van dezelfde vorm, nu met golfgetal k' en cirkelfrequentie $\omega'$ .

We veronderstellen dat we te maken hebben met een electromagnetische golf, een lichtgolf of een radiogolf, die zich in het vacuum voortplant. We nemen k>0. Uit |u|<c volgt k'>0. Voor electromagnetische golven geldt $\omega=c\vert k\vert$ , dus hier $\omega=ck$ . Voor k' hebben we dan

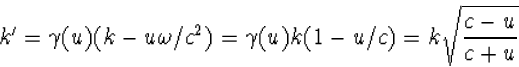$\begin{displaymath} k'=\gamma(u)(k-u\omega/c^2)=\gamma(u)k(1-u/c)=k\sqrt{\frac{c-u}{c+u}}\end{displaymath}$ (6.20)

en voor $\omega'$

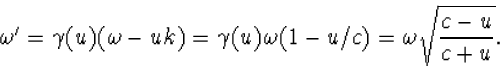$\begin{displaymath} \omega'=\gamma(u)(\omega-uk)=\gamma(u)\omega(1-u/c)=\omega \sqrt{\frac{c-u}{c+u}}.\end{displaymath}$ (6.21)

Voor de gewone frequentie $\nu$ vinden we op deze wijze

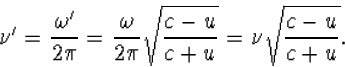$\begin{displaymath} \nu'=\frac{\omega'}{2\pi}=\frac{\omega}{2\pi}\sqrt{\frac{c-u}{c+u}}= \nu\sqrt{\frac{c-u}{c+u}}.\end{displaymath}$ (6.22)

Voor u>0 ziet een waarnemer in S' het systeem S van zich af bewegen. Voor u<0 ziet hij S juist naar zich toe bewegen. We concluderen:

Volgens de relativiteitstheorie wordt licht met frequentie $\nu$ ,dat wordt uitgezonden door een lichtbron die zich met een snelheid u>0 van ons af beweegt, door ons waargenomen als licht met de verlaagde frequentie

$\begin{displaymath} \nu'=\nu\sqrt{\frac{c-u}{c+u}}.\end{displaymath}$ (6.23)

Als de lichtbron met een snelheid v=-u>0 naar ons toe beweegt zien we de verhoogde frequentie

$\begin{displaymath} \nu'=\nu\sqrt{\frac{c+v}{c-v}}.\end{displaymath}$ (6.24)

Het Doppler-effect is niet iets dat alleen in een relativistische beschrijving van golfvoortplanting optreedt; we kennen het ook in de niet-relativistische fysica. Het kan immers gemakkelijk in het dagelijks leven om ons heen worden waargenomen, zoals we al aan het begin van dit hoofdstuk opmerkten. De verandering in waargenomen frequentie is natuurlijk verschillend. Om de niet-relativistische vorm van formule (6.23) te vinden gaan we opnieuw uit van de monochromatische 1-dimensionale golf van formule (6.15) die we weer beschrijven in twee inertiaal systemen S en S' . Het verband tussen deze systemen wordt nu gegeven door een Galilei transformatie (4.4). Met behulp van de inverse van deze transformatie vinden we in plaats van (6.17)

$\begin{displaymath} kx-\omega t=k(x'+ut')-\omega t'=k x'-(\omega-k u)t'\end{displaymath}$ (6.25)

en dus voor de nieuwe cirkelfrequentie

$\begin{displaymath} \omega'=\omega-ku.\end{displaymath}$ (6.26)

Voor een electromagnetische golf met k>0 wordt dit

$\begin{displaymath} \omega'=\omega(1-u/c).\end{displaymath}$ (6.27)

Het niet-relativistische analogon van (6.23) is dus

$\begin{displaymath} \nu'=\nu(1-u/c).\end{displaymath}$ (6.28)

Het is interessant om de relativistische en niet-relativistische formules voor het Doppler-effect met elkaar te vergelijken. Als u klein is ten opzichte van c kunnen we de relativistische formule (6.23) ontwikkelen naar machten van u/c. We krijgen dan

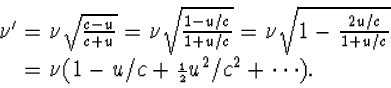$\begin{displaymath} \begin{array} {l} \nu'=\nu\sqrt{\frac{c-u}{c+u}}=\nu\sqrt{\f... ...}=\nu(1-u/c+{\scriptstyle{1\over 2}}u^2/c^2+\cdots).\end{array}\end{displaym ath}$ (6.29)

Het Doppler-effect voor licht is bij normale snelheden zeer klein, dit in tegenstelling tot wat we bij geluidsgolven waarnemen. In de relativistische zo wel als in de niet-relativistische theorie is het van de orde u/c. Het verschil tussen het niet-relativistische en relativistische effect is nog kleiner, namelijk van orde (u/c)².

We hebben ons in het voorafgaande bezig gehouden met een 1-dimensionale situatie. Als we de resultaten daarvan vertalen naar de 3-dimensionale wereld krijgen we een beschrijving van het z.g. longitudinale Doppler-effect: het effect dat optreedt als de snelheid van de lichtbron, gezien vanuit ons standpunt, geen tangentiële component heeft. In de astronomie heeft men de spectra gemeten van licht dat wordt uitgezonden door zeer ver van ons verwijderde melkwegstelsels. (Denk daarbij aan afstanden van de orde van 10⁸ à 10⁹ lichtjaren). De spectra die men op deze wijze vindt zijn de zelfde als die men kent uit de aardse fysica; ze vertonen alleen kleine verschuivingen naar het infra-rood. Dit is het gevolg van het Doppler-effect: de melkwegstelsels bewegen zich met grote snelheid van ons af. (Men concludeert op grond van de grootte van de gemeten Dopplerverschuivingen tot snelheden in de orde van 10⁴ km/s.) We kunnen gemakkelijk met behulp van de zojuist gevonden formules nagaan wat de verschuivingen in de frequenties van bijvoorbeeld de bekende waterstoflijnen bij een dergelijke snelheid zijn. Deze verschuivingen zijn zelf goed te meten, maar ze zijn vaak te klein om het verschil te zien tussen het relativistische en het niet relativistische effect.

Het Doppler-effect werd afgeleid door te laten zien hoe een monochromatische golfbeweging, die de amplitude van de golf op ieder tijdstip in ruimte en tijd geeft, transformeert. Er werd voor de eenvoud aangenomen dat die amplitude zelf in ieder inertiaalstelsel hetzelfde is. Voor een lichtgolf, die bestaat uit electromagnetische golven zult U later in de studie leren dat dit niet het geval is. De amplitude van een lichtgolf wordt beschreven door een electrisch (en een daarmee in tegenfase zijnde magnetisch) veld. Electrische en magnetische velden transformeren niet triviaal onder een Lorentz transformatie. Echter, ook een electromagnetische golf beschrijft een trilling waaraan een golflengte en een frequentie kan worden toegekend. Deze trilling hangt van plaats en tijd af via de combinatie $kx-\omega t$ (voor een vlakke golf in de x-richting) of in het algemeen van de combinatie $\vec k\cdot\vec x-\omega t= \sum_{i=1}^3k_ix_i-\omega t$ (voor een golf in een willekeurige richting $\vec k$ ). Bij de transformatie naar een ander inertiaalstelsel zal in het algemeen de amplitude van de golf op een niet triviale wijze transformeren, maar deze transformatie is op ieder punt langs de golf dezelfde. In het getransformeerde stelsel manisfesteert de golf zich weer als een golf, afhangende van plaats en tijd via de combinatie $\vec k{\,}'\cdot\vec x{\,}'- \omega' t'=\vec k\cdot\vec x-\omega t$ . Omdat we weten hoe $\vec x$ en t onder een Lorentz transformatie transformeren, kunnen we bepalen hoe $\vec k$ en $\omega$ transformeren, zoals eerder afgeleid, zie verg. (6.19). Voor een golfbeweging in een willekeurige richting $\vec k$ (onder een hoek $\theta$ met de x-richting) en een Lorentz transformatie (met een snelheid u in de x-richting) geldt dus

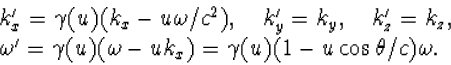$\begin{displaymath} \begin{array} {l} k_x^\prime=\gamma(u)(k_x-u\omega/c^2),\qua... ...ma(u)(\omega-uk_x)=\gamma(u)(1-u\cos\theta/c)\omega.\end{array}\end{displaym ath}$ (6.30)

Opgave 17:

Controleer dat $\vec k{\,}'\cdot\vec x{\,}'-\omega' t' =\vec k\cdot\vec x-\omega t$ .

We kunnen nu eenvoudig het Doppler-effect bepalen voor een golf langs de x-as (dus in de richting van de relative beweging tussen bron en waarnemer), of dwars daarop. Laten we eerst het laatste geval bestuderen; we spreken dan van een transversaal Doppler-effect. Omdat nu $\vec k$ loodrecht staat op de bewegingsrichting (de x-richting) geldt k_x=0, zodat $\omega'=\gamma(u)\omega$ . Onder een Galilei transformatie zou de factor $\gamma(u)$ afwezig zijn, en in de Newtonse theorie is er geen transversaal Doppler-effect. We zien dus dat voor een transversaal bewegende bron (of waarnemer) de waargenomen frequentie groter is dan in het ruststelsel.

Het Doppler-effect kan ook fysisch verklaard worden door op te merken dat de tijd $\Delta t$ tussen twee golfdalen precies als de duur van een tik van een klok gezien kan worden. Voor een bewegende bron nemen we een langzamer verlopende tijd waar, aanleiding gevende tot een langere periode $\Delta t'=\gamma(u)\Delta t$ tussen twee golfdalen. Maar als de bron (waarnemer) zich ook nog eens met een snelheid u van de waarnemer (bron) af beweegt, dan doet een tweede golfdal er $u\Delta t'/c$ langer over om aan te komen. Immers de bron (waarnemer) heeft tussen twee tikken een afstand $u\Delta t'$ afgelegd, en de golf doet er $u\Delta t'/c$ seconden over om die extra afstand te overbruggen. Als de beweging tussen bron en waarnemer niet langs de richting van waarneming plaats vindt, maar onder een hoek $\theta'$ daarmee, dan is de extra tijd tussen twee tikken uiteraard $u\Delta t'\cos\theta'/c$ . We vinden derhalve $\Delta t'=\gamma(u)(1+u\cos\theta'/c)\Delta t$ .Met een cirkelfrequentie $\omega=2\pi\nu$ , bepaald door $2\pi/\Delta t$ , volgt

$\begin{displaymath} \omega'=\omega/\left[\gamma(u)(1+u\cos\theta'/c)\right].\end{displaymath}$ (6.31)

Voor $\theta'=0$ vinden we nu het eerder gevonden resultaat: als de bron met een snelheid u van de waarnemenr af beweegt wordt de frequentie kleiner met een factor $\sqrt{(c-u)/(c+u)}$ . (De golflengte wordt dus groter en we spreken van een roodverschuiving). Maar voor het transversale Doppler-effect vinden we nu dat de frequentie eveneens kleiner wordt, terwijl we eerder het omgekeerde hadden geconcludeerd.

Dat kan natuurlijk niet. Wat is hier aan de hand zult U zich afvragen? De oplossing zit hem wederom in het feit dat we ons heel goed moeten afvragen wat we meten. In de eerste afleiding van het transversale Doppler-effect is de hoek $\theta$ de hoek met de bewegingsrichting in het stelsel waarin de bron in rust is. In de tweede afleiding, bezien vanuit het standpunt van de waarnemer, is $\theta'$ de hoek voor de richting waaruit het signaal afkomstig is, in het stelsel waarin de waarnemer in rust is. Als de relatieve beweging tussen bron en waarnemer in de signaalrichting plaats vindt dan zijn die hoeken uiteraard gelijk ( $\theta=\theta'=0$ ). Bij het transversaal Doppler-effect is dit niet het geval.

Opgave 18:

Gegeven dat beide uitdrukkingen voor de transformatie van $\omega$ , $\omega'=\omega\gamma(u)(1-u\cos\theta/c)$ en $\omega'= \omega/[\gamma(u)(1+u\cos\theta'/c)]$ , correct zijn. Laat zien dat $\cos\theta'=(\cos\theta-u/c)/(1-u\cos\theta/c)$ .

Dit heet (relativistische) aberratie, welbekend uit de sterrenkunde, waar de varierende richting van de beweging van een aardse waarnemer door draaiing van de aarde om de zon (en in mindere mate door de draaiing om haar as) tot kleine schommelingen in de positie van de sterren aanleiding geeft (de maximale afwijking bedraagt iets meer dan 20 boogseconden).

Merk op dat $\omega'=\omega/\left[\gamma(u)(1+u\cos\theta'/c)\right]$ ook als $\omega=\gamma(u)(1+u\cos\theta'/c)\omega'$ geschreven kan worden. Dit is precies de inverse transformatie van S' naar S, in plaats van S naar S'. Juist deze inverse transformatie is relevant als we uitgaan van de situatie van de waarnemer! Er zijn maar weinig leerboeken die bij het transversaal Doppler-effect aandacht besteden aan de vraag wat we nu precies met transversaal bedoelen. Dat is waarom we er hier wat uitvoeriger op ingaan. Altijd weer moeten we ons vragen wat het meetproces is. Dus eerst denken, dan rekenen.

Het relativistische Doppler-effect, inclusief het transversale effect, werd al in 1938 nauwkeurig gemeten door Ives en Stilwell. In de jaren '60 is dit nog eens overgedaan, gebruik makende van een op de uiteinden van een rotor opgestelde bron (of detector) van gammastraling, gebruikmakende van het Mössbauer effect. Dit effect is gebaseerd op het feit dat in een vaste stof bij absorbtie van de (gamma)straling de terugstoot verdeeld wordt over het hele materiaal (door de binding van het atoom aan de rest). Hierdoor kan de energie van het foton heel nauwkeurig worden vastgelegd (er is geen verbreding van de absorbtielijn, zoals bij losse atomen in een gas).

6.7 INTERMEZZO (gravitationele roodverschuiving)
Als we nu terugdenken aan ons roterend ruimtestation, dan zien we dat het transversale Doppler-effect een eenduidige relatie met de zogenaamde gravitationele roodverschuiving heeft. Straling afkomst van een ster heeft een kleine roodverschuiving door het gravitatieveld van de ster. Evenzo is licht dat op het aardoppervlak wordt uitgezonden en boven in een hoge toren wordt waargenomen, ook een heel klein beetje naar het rood verschoven. Dit is de basis van een van de klassieke tests geweest van Einstein's algemene relativiteistheorie, zoals uitgevoerd door Pound en Rebka in 1960. Ook hier werd van het Mössbauer effect gebruik gemaakt. Bron en detector waren op een hoogte van 21,6 meter ten opzichte van elkaar opgesteld. Pound en Rebka waren in staat de voorspelde verschuiving, $\Delta\omega/\omega=2,56\times 10^{-15}$ te meten! (Probeer de grootte van dit effect zelf na te rekenen).

Volgende hoofdstuk

Naar inhoudsopave