3. Inertiaalsystemen

We gaan eens wat nauwkeuriger kijken naar de situatie zoals die optreedt bij de rijdende trein waar we eerder over spraken. Dus twee waarnemers die zich ten opzichte van elkaar eenparig rechtlijnig bewegen. Ieder van de twee waarnemers heeft voor zich zelf een ruimtelijk assenstelsel dat met hem meebeweegt. Een natuurlijk assenstelsel is een z.g. Euclidisch assenstelsel, met rechthoekige ruimtelijke coördinaten. Voorwerpen kunnen worden gedraaid en verschoven; hun meetkundige eigenschappen veranderen daarbij niet; er is in de ruimte om ons heen een evident begrip van lengtes en hoeken. De plaats van de oorsprong van het assenstelsel doet er niet toe en ook de richting van de assen niet. We nemen aan dat onze beide waarnemers zich ieder in zo'n rechthoekig assenstelsel bevinden, en dat ze beiden over een klok van het zelfde type beschikken. Ze kunnen dan allebei elementaire metingen doen. Ze kunnen lengtes, tijdsintervallen en dus ook snelheden bepalen. In de situatie waarbij de ene waarnemer zich in een met constante snelheid rijdende trein bevindt en de andere er buiten een stationaire positie gekozen heeft, nemen ze allebei het zelfde belangrijke feit waar:

Een voorwerp dat aan zich zelf wordt overgelaten, d.w.z. waarop geen krachten werken, blijft in rust of beweegt zich eenparig rechtlijnig. Dit suggereert de volgende definitie:

Een Euclidisch ruimtelijk coördinaatstelsel waarin een aan zich zelf overgelaten voorwerp in rust blijft of eenparig rechtlijnig beweegt noemen we een inertiaalsysteem.

De twee waarnemers bevinden zich dus in twee verschillende inertiaalsystemen. Voor de waarnemer in de trein geldt dat zolang de trein met constante snelheid rijdt. Zodra de trein afremt of door een bocht gaat beginnen losliggende voorwerpen om hem heen ``vanzelf'' te bewegen; zijn coördinaatstelsel is dan géén inertiaalstelsel meer.

Opmerking: Het begrip inertiaalsysteem is natuurlijk een idealisatie, net zoals begrippen als puntmassa, wrijvingsloze beweging, etc. We moeten daarbij allerlei storende omstandigheden wegdenken.

Met behulp van het begrip inertiaalsysteem kunnen we nu het al genoemde relativiteitsprincipe precieser formuleren:

De natuurwetten hebben in elk inertiaalsysteem de zelfde vorm; ze zijn het zelfde.

Dit betekent dat alle inertiaalsystemen onderling equivalent zijn. Het betekent ook dat beweging relatief is in de zin dat er geen absoluut onderscheid gemaakt kan worden tussen rust en eenparig rechtlijnige beweging.

Beschouw nu een inertiaalsysteem S met ruimtelijke coördinaten x, y, z, en daarin een puntdeeltje waarop geen krachten werken. (We veronderstellen dat er geen zwaartekracht is). De beweging van het deeltje wordt beschreven door de formule
$\vec r(t)=\vec v t+\vec r(0),$ (3.1)

of uitgeschreven
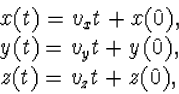$\begin{array} x(t)=v_x t+x(0),\\ y(t)=v_y t+y(0),\\ z(t)=v_z t+z(0), \end{array}$ (3.2)

met daarin $\vec v=(v_x,v_y,v_z)$ een constante snelheid, die eventueel nul mag zijn waardoor de situatie met het deeltje in rust als speciaal geval is ingesloten. Stel dat we een tweede coördinaatstelsel S' hebben, met ruimtelijke coördinaten x', y', z', dat zich eenparig rechtlijnig beweegt ten opzichte van het stelsel S, en wel met snelheid $\vec u=(u_x,u_y,u_z)$ . We kunnen dan op tijdstip t de coördinaten x', y', z' uitdrukken in de x, y, z volgens
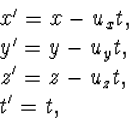
$\begin{array} x'=x-u_x t,\\ y'=y-u_y t,\\ z'=z-u_z t,\\ t'=t,\end{array}$ (3.3)

We hebben daarbij nog aangenomen dat op het tijdstip t=0 de oorsprongen van de twee stelsels samenvallen, anders zouden de formules nog constante termen bevatten. We kunnen de formules die de beweging van het deeltje beschrijven van de coördinaten x, y, z vertalen naar x', y', z'. We krijgen
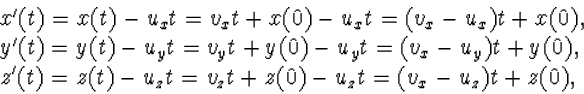
$\begin{array} x'(t)=x(t)-u_xt=v_xt+x(0)-u_xt=(v_x-u_x)t+... ...\ z'(t)=z(t)-u_zt=v_zt+z(0)-u_zt=(v_x-u_z)t+z(0),\\ \end{array}$ (3.4)

dus weer een eenparig rechtlijnige beweging, nu met constante snelheid
$\vec v{\,}'=\vec v-\vec u=(v_x-u_x,v_y-u_y,v_z-u_z).$ (3.5)

We zien daarmee op de eerste plaats dat ook S' een inertiaalstelsel is. In beide stelsels gelden de zefde wetten van de mechanica. Wij kunnen bijvoorbeeld eenvoudig nagaan dat bij de transformatie van S naar S' de fundamentele Newtonse wet die de beweging van een deeltje beschrijft niet verandert. Deze wet luidt
$\vec F=m\vec a.$ (3.6)

Daarbij is m de massa van een het deeltje, $\vec F$ de kracht die er op werkt en $\vec a$ de versnelling die daar het gevolg van is. In S beschrijven we de beweging van het deeltje met $\vec r(t)$ . Daarbij horen snelheid en versnelling.
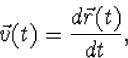$\vec v(t)=\frac{d\vec r(t)}{dt},$ (3.7)

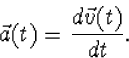$\vec a(t)=\frac{d\vec v(t)}{dt}.$ (3.8)

In S' wordt de beweging van het zelfde deeltje beschreven met
$\vec r{\,}'(t)=\vec r(t)-\vec u t,$ (3.9)

en dus met snelheid en versnelling
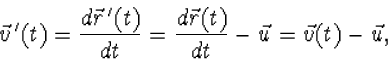$\vec v(t)=\frac{d\vec r(t)}{dt},$ (3.10)

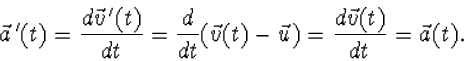$\vec a(t)=\frac{d\vec v(t)}{dt}.$ (3.11)

Aangezien m en $\vec F$ niet veranderen geldt $\vec F = m\vec a$ in S en $\vec F = m\vec a{\,}'$ in S'.

Transformaties van het type (3.3) noemen we Galilei transformaties. We zeggen dat de Newtonse mechanica Galilei invariant is.

Uit het voorafgaande kunnen we ook nog de volgende algemene conclusie trekken: Een eenparig rechtlijnige beweging die in een gegeven inertiaalstelsel S een snelheid $\vec v$ heeft wordt in een tweede inertiaalstelsel S' dat ten opzichte van het eerste met een constante snelheid $\vec u$ beweegt waargenomen als een eenparig rechtlijnige beweging met snelheid $\vec v-\vec u$ .Voor de algemene relativiteitstheorie kan het relativiteitsprincipe uitgebreid worden tot de opmerking dat men lokaal geen onderscheid kan maken tussen een versnelling en een gravitatieveld. Dit helpt ook om een inertiaalstelsel iets minder abstract te definiëren als het stelsel van vrije val (m.a.w. er werken geen netto krachten). Zo'n stelsel wordt ook wel een lokaal inertiaalstelsel (of lokaal Lorentz stelsel) genoemd. Een voorbeeld is een ruimteschip als de Mir, waar de astronauten geen zwaartekracht ondervinden (ze zijn in hun baan om de aarde constant in vrije val - alternatief kan men zeggen dat de zwaartekracht wordt opgeheven door de centrifugale kracht). Er is wel een heel kleine getijdekracht, omdat de balans strikt gesproken alleen voor het zwaartepunt van het ruimteschip dient (daarnaast is er een ``schijnkracht'' t.o.v. het zwaartepunt tengevolge van de centrifugale kracht). Voor de getijdekracht geldt dat deze evenredig is met de afmeting van het ruimtestation, gedeeld door de derde macht van de afstand tot het centrum van de aarde.

Opgave 1:

Bereken de grootte van de residuele kracht t.o.v. het zwaartepunt door getijde en centrifugale kracht mee te nemen. Kies zelf voor de baan van de Mir een realistische waarde. U zult nu begrijpen waarom een ruimteschip (en een vrij vallende lift) een goede benadering voor een inertiaalsysteem zijn.

In vergelijking (3.3) voor de Galilei transformaties is de fundamentele aanname gemaakt dat t'=t, m.a.w. dat er een universeel gedefinieerde tijd bestaat (zie ook par. 4). Echter voor het meten van de tijd op verschillende plaatsen moeten we de stand van de klokken vergelijken en voor het vergelijken moeten we informatie uitwisselen. Dit geldt evenzeer voor het meten van de lengte van een meetlat. In het dagelijks leven komt deze vergelijking tot stand door het proces van kijken (naar de wijzers van het uurwerk), maar stel dat we blind waren, dan moeten we eerst naar de klok om de stand te controleren. Bij ver verwijderde klokken kost dat een aanzienlijke tijd en als we na het gelijkzetten van de klokken terug gaan naar onze oorsponkelijke plaats wordt de stand van de klok gededuceerd door te corrigeren voor de tijd die we nodig hadden om terug te keren op onze plaats. Dat zijn in dit geval aanzienlijke correcties waarvoor we precies moeten weten wat onze snelheid was. Zo ook moeten we dus precies weten wat de snelheid van het licht is. Als deze oneindig is, kunnen we klokken instantaan gelijk zetten.

Het was Ole Roemer die in 1676 voor het eerst aantoonde dat licht een eindige snelheid heeft. Hij deduceerde dit door zorgvuldig het tijdstip bij te houden, waarop de maan Io binnentreedt in de schaduw van de planeet Jupiter, waar Io in 1,77 dagen omheen loopt. Door de situatie tijdens oppositie (waar de aarde tussen zon en Jupiter in staat) en conjunctie (waar de zon tussen aarde en Jupiter staat - en we dus Jupiter maar moeizaam kunnen waarnemen) met elkaar te vergelijken ontdekte Roemer dat er een discrepantie was die verklaard kon worden door aan te nemen dat het licht er ca. 22 minuten voor nodig had om de aardbaan te doorkruisen, oftewel een afstand af te leggen van 2 A.E. (Astronomische Eenheden). Met 1 A.E. de gemiddelde afstand van de aarde tot de zon, bepaald op ca. 150 miljoen km, kwam Christiaan Huygens twee jaar later uit op een snelheid van 200.000 km/s. In feite is de snelheid van het licht ca. 300.000 km/s, zodat Roemer een systematische fout had (in werkelijkheid heeft het licht 16 à 17 minuten nodig om de aardbaan te doorkruisen).

Opgave 2:

Als we de tijd meten waarop Io samenvalt met de rand van Jupiter, laat dan zien dat zonder rekening te houden met de eindigheid van de lichtsnelheid, er ook een tijdsverschil optreedt als de aarde zich midden tussen oppositie en conjugatie bevindt, en dat dit tijdsverschil (met oppositie of conjugatie) op kan lopen tot ca. 1,3 uur (zowel voor als achter). De afstand van Jupiter tot de zon bedraagt 5,2 A.E. (we nemen voor het gemak alle banen cirkelvormig).

Tot zover hebben we alleen gekeken naar de mechanica. Nu het electromagnetisme. Licht is een golfverschijnsel van electromagnetische aard, dat zich volgens een uit de Maxwell vergelijkingen afgeleide golfvergelijking voortplant. Vanuit een centrale lichtbron breidt het licht zich bolvormig naar alle kanten uit. De punten van het golffront bewegen zich daarbij volgens rechte lijnen. Dit zijn de lichtstralen. Licht in deze zin beweegt zich dus rechtlijnig en met een snelheid die volgens de Maxwell vergelijkingen in vacuum een zeer bepaalde constante waarde heeft. Als het relativiteitsprincipe ook voor de Maxwelltheorie geldt moeten de Maxwellvergelijkingen in S en S' dezelfde gedaante hebben. Daaruit zou weer volgen dat een lichtstraal in S en S' dezelfde snelheid heeft. Dit is duidelijk in strijd met de hierboven uitgesproken algemene conclusie. We gaan hier nader op in. Al in het begin van de 19e eeuw was men, vooral op grond van waargenomen buigings en interferentie effecten, tot de overtuiging gekomen dat licht een golfverschijnsel was. De golftheorie van het licht kreeg een verdere expliciete vorm binnen de algemene theorie van het electromagnetisme die in 1864 door J.C. Maxwell werd geformuleerd. Licht was een electromagnetische golf, met voor ieder medium en ook voor het vacuum een vaste voortplantingssnelheid. Een voor de hand liggende vraag was wat de drager van deze golven was. Watergolven zijn golven in water, geluidsgolven planten zich voort in lucht of in een andere stof. Lichtgolven planten zich daarentegen ook voort in het luchtledige. Dit leidde tot de veronderstelling dat er een universeel medium was, overal aanwezig, ook in het vacuum, dat als drager voor de electromagnetische golven fungeerde. Dit hypothetische zeer ijle medium noemde men de ether. De constante lichtsnelheid in het vacuum, die door de vergelijkingen van Maxwell voorspeld werd, was dan de voortplantingssnelheid ten opzichte van de ether. De aanwezigheid van deze ether, die een absolute standaard voor rust en beweging introduceerde, ging wel in tegen het relativiteitsprincipe, waaraan de Newtonse mechanica voldeed. Niet alle inertiaalsystemen waren meer equivalent; er was één speciaal systeem, namelijk het systeem bepaald door de ether. Men dacht daarbij dat dit in de een of andere zin werd vastgelegd door het geheel van de vaste sterren in het heelal. De aarde, de zon en het planetenstelsel zouden zich dan bewegen ten opzichte van de ether. Deze beweging zou experimenteel kunnen worden vastgesteld. Dit was het doel van een vernuftig en zeer nauwkeurig experiment dat in 1881 door de Amerikaanse fysicus A.A. Michelson alleen en in 1887 samen met zijn landgenoot E.W. Morley werd uitgevoerd.

We vatten nog even samen: Op zich hoeft het eindig zijn van de lichtsnelheid geen probleem op te leveren met de Galilei invariantie, zolang het licht zich gedraagt zoals we van golven zouden verwachten: ze planten zich voort in een medium en dat medium definieert het referentiekader waaraan we alle beweging kunnen relateren. Voor geluids- en watergolven hangt de golfsnelheid niet af van de snelheid van de bron, maar wel van die van de waarnemer t.o.v. van het medium (uiteraard hangt de frequentie wel af van de snelheid van de bron, zoals we ook later bij het dopplereffect voor licht zullen bespreken). Het is echter de vraag of lichtgolven zich werkelijk gedragen als geluidsgolven, d.w.z. of er echt een ether bestaat. Het experiment van Michelsen en Morley heeft aangetoond dat er inderdaad geen ether is (of dat het licht zich er niets van aantrekt). Het is een ietwat vreemde misconceptie geweest te denken dat lichtgolven een ether nodig hebben. De Maxwellvergelijkingen beschrijven deze golven in vacuum zonder één porbleem, waar het principe gebaseerd is op het feit dat een tijdsafhankelijk elektrisch veld een tijdsafhankelijk magnetisch veld genereert, wat op zijn beurt weer een tijdsafhankelijk electrisch veld genereert en zich alsdus voortplant. Hiervoor is de tussenkomst van een medium niet nodig.

Vóór de bespreking van het Michelson en Morley experiment is het dan ook mogelijk om al aan te geven dat de Maxwell theorie kuren vertoont als we een Galilei transformatie toepassen. Het was deels om deze kuren te omzeilen dat Lorentz zijn nu beroemde transformatie introduceerde, zodanig dat de Maxwellvergelijkingen eronder invariant zijn (Lorentz heeft er niet de algemene geldigheid, met haar consequenties voor ruimte en tijd, in onderkend en het was Einstein die het onderliggende principe bloot heeft weten te leggen). Aan een heel eenvoudig voorbeeld kunnen we zien dat er inderdaad bij electromagnetisme problemen met de Galilei invariantie optreden.

Beschouw hiertoe twee deeltjes met lading q op een afstand r die een Coulomb afstoting voelen ter grootte van $F=q^2/(4\pi \epsilon_o r^2)$ . Door een bewegende waarnemer wordt naast de Coulomb afstoting echter ook een aantrekkende kracht gezien, die samenhangt met het feit dat een bewegende lading een electrische stroom representeert en dat twee evenwijdig stromen elkaar aantrekken. Deze aantrekkingswet vormt de definitie van de Ampère, die luidt dat de kracht die een stroomdraad per meter ondervindt van een daaraan evenwijdige stroomdraad met dezelfde stroomsterkte I op een afstand van een meter precies een kracht van 2.10^-7 N ondervindt indien I=1 A. Als het goed is kent U deze wet nog van de middelbare school, $F_A=\mu_o I^2/(2\pi r)$ . Wat heeft dat met ons probleem hier te maken zult U zich afvragen? Immers bij een stroomdraad wordt ten eerste de Coulomb afstoting afgeschermd, doordat de stroomdraad neutraal is (alleen de negatief geladen elektronen worden getransporteerd). Verder is de stroom qv lokaal, en strekt deze zich niet uit langs een hele draad. De kracht is in dit geval dan ook niet evenredig met 1/r, maar met 1/r², $F_s=\mu_o q^2v^2/(4\pi r^2)$ . Net als bij de stroomdraden wordt deze aantrekkende kracht, gericht langs de verbindingslijn tussen de twee bewegende ladingen, veroorzaakt door het feit dat een bewegend electrisch veld een magnetisch veld veroorzaakt en dat de andere bewegende lading een Lorentz kracht ondervindt tengevolge van dit magneetveld.

Opgave 3:

Laat zien dat uit $F_s=\mu_oq_1v_1q_2v_2/(4\pi r_{12}^2)$ (gericht langs de verbindingslijn tussen de twee ladingen met als afstand r₁₂ tussen deze ladingen) de wet van Ampère volgt. Gebruik hierbij

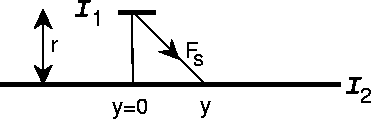
dat de stroomdraden opgebouwd kunnen worden uit bewegende ladingspakketjes, $qv=I\Delta \ell$ , zodat de kracht die de stroom I₁ op een stukje stroomdraad ter lengte $\Delta\ell_1$ voelt ten gevolge van de stroomdraad I₂ gegeven wordt door

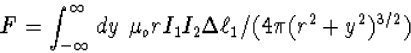
$F= \int^\infty_{-\infty}dy~\mu_or I_1 I_2\Delta\ell_1/(4\pi(r^2+y^2)^{3/2})$

(Hierin speelt dus I₂dy de rol van q₂v₂ en wordt de totale kracht verkregen door alle stukjes dy bij elkaar op te tellen - te integreren dus).

Nu we ons verzekerd hebben van de juistheid van de extra aantrekkende kracht, concluderen we dus dat de bewegende waarnemer een totale kracht ziet die gegeven wordt door F_v=(1-v²/c²)F, waar F de kracht in het ruststelsel (de Coulomb kracht) is. Dit is niet wat we van een Galilei transformatie zouden verwachten.

We hebben de opstelling van het Michelson en Morley experiment schematisch voorgesteld in figuur 3.1.

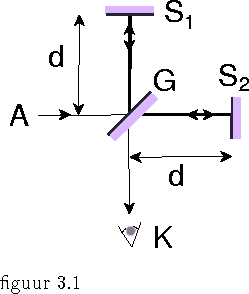
Het licht van een ster A komt het apparaat binnen en valt op een schuin geplaatste glazen plaat G die met een gedeeltelijk doorlatende metaallaag is bedekt. De helft van het licht wordt onder een hoek van 90 graden gereflecteerd, gaat naar de spiegel S₁, wordt daar teruggekaatst en keert weer bij de glasplaat G terug. De andere helft gaat ongehinderd door G heen, wordt vervolgens door de spiegel S₂ teruggekaatst en komt ook weer bij G terug. Er ontstaat een interferentie effect dat met behulp van een kijker K kan worden waargenomen. De twee armen van deze z.g. Michelson interferometer zijn even lang. Het apparaat kan tijdens het experiment nog over een hoek van 90 graden worden gedraaid, waardoor de rol van beide armen verwisseld wordt. De interferometer beweegt zich met de aarde in een baan om de zon, met een snelheid van ongeveer 30 km/s. Afhankelijk van de positie van de aarde in haar baan, dus van de tijd van het jaar, kan deze snelheid naar de ster toe of er vandaan gericht zijn. Volgens de hypothese die men met dit experiment wil testen, heeft het licht een constante snelheid ten opzichte van de ether en beweegt het meetapparaat zich door de ether daartegen in of in de zelfde richting mee. In beide gevallen betekent dit dat de snelheid van het licht in het apparaat langs de as naar S₁ en terug, en in transversale richting naar S₂ en terug, verschillend zijn en dat dus de optische weglengten langs beide armen verschillend zijn. De nauwkeurigheid van het experiment is ruim voldoende om het interferentie effect te meten dat hiervan het gevolg zou zijn.

Het Michelson-Morley experiment heeft afgerekend met het idee van de ether. Het beoogde effect werd niet waargenomen, zoiets heet een nulresultaat. In de praktijk werd in plaats van sterlicht een aan de opstelling bevestigde lichtbron gebruikt, immers de snelheid van de bron beinvloedt in een ethertheorie de lichtsnelheid niet. Stel nu dat we de ether vergelijken met een rivier, die horizontaal naar links een stroomsnelheid heeft van 3 m/s. De fotonen die tussen het halfdoorlatende spiegeltje G en de spiegels S₁ en S₂ heen en weer lopen kunnen we vergelijken met een speedboat, die we een snelheid van 5 m/s geven. Als we beide afstanden 100 m veronderstellen, dan is de vraag welke boot het eerste terug is bij de spiegel G. Voor de boot die bij S₂ keert is de verstreken tijd 100/2+100/8 s=50+12,5 s (op de heenreis is het tegen de stroom in ploeteren met een snelheid van 2 m/s, terwijl op de terugreis een flitsende 8 m/s wordt bereikt). Voor de boot die bij S₁ keert, kost het wat moeite om niet met de stroom af te drijven en moet de boot zijn steven dus in de richting van de stroom draaien, precies zodanig dat de snelheidscomponent gericht tegen de stroom in 3 m/s bedraagt. Er blijft dan dus gebruikmakende van de stelling van Pythagoras slechts 4 m/s over voor het afleggen van de te overbruggen afstand. De verstreken tijd is nu dus 2*100/4s=50 s, ruimschoots sneller dan de andere boot.

Als we nu de snelheid van de boot vervangen door de lichtsnelheid c, de stroomsnelheid door de snelheid v van de ether en de af te leggen afstand door d, dan kost de reis van G naar S₂ en terug 2cd/(c²-v²) s en de reis van G naar S₁ en terug, dwars op de richting van de ether, kost $2d/\sqrt{c^2-v^2} s$ . Van te voren kon men niet weten hoe hard en uit welke richting de ether zou waaien. Het zou dus toevallig op de dag van meting windstil geweest kunnen zijn. Echter de aarde beweegt om de zon met een snelheid van 30 km/s, zodat er slechts op een heel bepaalde dag van het jaar mogelijk geen etherwind is (die dan zelf ook 30 km/s t.o.v. de zon moet bedragen, uiteraard ervan uitgaande dat het etherweer stabiel is over de tijdsduur van een jaar). Het nulresultaat was totaal onverwacht en het verhaal gaat dat Michelson, toen al een beroemd experimentator, voor elkaar heeft gekregen op een dag in 1887 in Cleveland Ohio al het tramverkeer stil te leggen om de trillingen in de interferometer te minimaliseren!

Lorentz en FitzGerald hebben onafhankelijk van elkaar geprobeerd het nulresultaat te verklaren door aan te nemen dat de interferometerarm, die in de richting van de etherwind wijst, een contractie ondergaat met een factor $\sqrt{1-v^2/c^2}$ . Als de arm niet precies in de richting van de etherwind wijst, moet men voor v de component in de richting van de arm nemen bij het berekenen van de contractie. De volgende opgave (gebaseerd op een experiment uit 1932 door Kennedy en Thorndike) laat zien dat voor gelijke armen dit inderdaad het nulresultaat verklaart, maar dat zodra de armen van ongelijke lengte zijn er ook met de Lorentz-FitzGerald contractie een variatie t.g.v. de etherwind te verwachten is.

Opgave 4:

Laat zien dat voor een interferometer met armen van lengte d₁ en d₂, waarbij de etherwind een hoek $\alpha$ met de eerste arm maakt, het tijdsverschil voor de looptijd in de twee armen, die verondersteld worden een contractie te ondergaan bepaald door de snelheidscomponent gericht langs de armen, de volgende afhankelijkheid van $\alpha$ en v vertoont:

$2c^{-1}(1-v^2/c^2)^{-1}(d_1-d_2)\sqrt{1-v^2\cos\!{}^2\alpha/c^2} \sqrt{1-v^2\sin{}^2\alpha/c^2}.$

Merk op dat dit tijdsverschil inderdaad verdwijnt bij een interferometer met gelijke armen!

Naast de contractie van lengte heeft men ook een zg. tijdsdilatie nodig, maar op het moment dat we die ook in rekening brengen kunnen we het resultaat ook samenvatten zoals Einstein dat deed, en strikt gesproken Maxwell ons al die tijd heeft proberen te vertellen:

Het lichtpostulaat:
De lichtsnelheid heeft in ieder (lokaal) inertiaalstelsel dezelfde waarde.

Door de toevoeging van het woord lokaal geldt dit postulaat ook in de aanwezigheid van gravitatie!

Dus voor Einstein betekende het nulresultaat dat de ether moest worden opgegeven en dat men van de voortplanting van licht, en van electromagnetische verschijnselen in het algemeen, alleen kon zeggen dat de voortplantingssnelheid in ieder inertiaalsysteem de zelfde was. Het relativiteitsprincipe gold dus ook voor deze verschijnselen; het moest een algemeen geldig fysich principe zijn. De schijnbare discrepantie tussen het relativiteitsprincipe en het constant zijn van de lichtsnelheid zou moeten worden opgeheven door de overgang tussen twee inertiaalsystemen op een nieuwe manier te beschrijven.

We vatten het voorafgaande nog even kort samen: Uit Maxwell's algemene theorie van het electromagnetisme en de experimenten van Michelson en Morley volgt dat licht een electromagnetisch golfverschijnsel is dat zich in een inertiaalstelsel met een constante snelheid voortplant. In vacuum is dat ongeveer 300.000 km/s, om iets preciezer te zijn 299.793 km/s. Dit is een natuurconstante die men c noemt. Op grond van de eerder gegeven redenering over het verband tussen de snelheden van een bewegend deeltje waargenomen in verschillende inertiaalsystemen zou men een ander resultaat verwacht hebben: Als een lichtgolf zich in inertiaalstelsel S met snelheid $c\vec e$ beweegt, met $\vec e$ een eenheidsvector, dan zou die zelfde golf in een tweede stelsel S', dat zich t.o.v. S met een snelheid $\vec u$ beweegt, de snelheid $c\vec e-\vec u$ , dus met grootte $\vert c\vec e-\vec u\vert$ , moeten hebben. Deze paradox is door Einstein opgelost met behulp van zijn speciale relativiteitstheorie. De grondgedachte daarbij is een nieuwe en nu algemeen aanvaarde interpretatie van het relativiteitsprincipe, met andere transformatieformules voor de relatie tussen twee inertiaalstelsels. Dit gaan we in het volgende hoofdstuk uiteenzetten.

Volgende hoofdstuk

Naar inhoudsopave